Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:08:11.093Z Has data issue: false hasContentIssue false
  • English
  • Français

On Pták's double-limit theorems

Published online by Cambridge University Press:  20 January 2009

N.J. Young
N.J. Young
Affiliation:
The University, Glasgow, W.2
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider uniform spaces X and Y and a separately uniformly continuous real-valued function f on X × Y. The following question arises in the theory of games: under what conditions can f be extended to a separately continuous function on 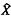× Ŷ, where 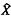, Ŷ are the completions of X and Y respectively? Firstly observe that such an extension is not always possible. If X = Y = (0, 1] with the usual uniform structure and f(x, y) = xy then f is separately uniformly continuous but has no separately continuous extension to 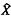× Ŷ = [0, 1]2 since such an extension would satisfy f(0, .) = 0 on Y and f(., 0) = 1 on X and so would necessarily have a discontinuity in one argument at the origin.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 17 , Issue 3 , June 1971 , pp. 193 - 200
Copyright
Copyright © Edinburgh Mathematical Society 1971

References

REFERENCES

(1)Dunford, N. and Schwartz, J. T., Linear Operators, Part 1 (Interscience. 1958).Google Scholar
(2)Gillman, L. and Jerison, M., Rings of Continuous Functions (Van Nostrand, 1960).CrossRefGoogle Scholar
(3)GRothendieck, A., Sur la complétion du dual d'un espace localement convexe, C.R. Acad. Sci. Paris 230 (1950), 605–606.Google Scholar
(4)Grothendieck, A., Critères de compacité dans les espaces fonctionnels généraux, Amer. J. Math. 74 (1952), 168–186.CrossRefGoogle Scholar
(5)Köthe, G., Topologische Lineare Räume I (Springer Verlag, 1960).CrossRefGoogle Scholar
(6)Pták, VL., An extension theorem for separately continuous functions and its application to functional analysis, Czechoslovak Math. J. 14 (89) (1964), 562–581.CrossRefGoogle Scholar
(7)Pták, VL., A combinatorial lemma on the existence of convex means and its application to weak compactness, Proc. Sympos. Pure Math. Vol. VII (American Math. Soc, Providence, R.I., 1963), 437–450.Google Scholar
(8)Robertson, A. P. and Robertson, W. J., Topological Vector Spaces (Cambridge University Press, 1964).Google Scholar