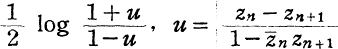Research Article
Theta Functions and Abelian Varieties over Valuation Fields of Rank one I
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-27
-
- Article
-
- You have access
- Export citation
Problèmes D’universalité s’Introduisant dans l’Algébrisation de la Logique Mathématique I
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-73
-
- Article
-
- You have access
- Export citation
Dirichletsche Abbildungen
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 75-89
-
- Article
-
- You have access
- Export citation
A Maximal Riemann Surface
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 91-93
-
- Article
-
- You have access
- Export citation
On the Boundary Behavior of Holomorphic Functions in the Unit Disk
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 95-103
-
- Article
-
- You have access
- Export citation
A Theory of Mathematical Objects as a Prototype of Set Theory
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 105-168
-
- Article
-
- You have access
- Export citation
Strongly Regular Extensions of Rings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 169-183
-
- Article
-
- You have access
- Export citation
A Remark on Orthogonality Relations in Finite Groups
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-194
-
- Article
-
- You have access
- Export citation
R-Sequences and Homological Dimension1)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 195-199
-
- Article
-
- You have access
- Export citation
A Theorem on Factorizable Groups of Odd Order
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 201-203
-
- Article
-
- You have access
- Export citation
Correction
Correction to our Paper “On Frobenius Extensions II”
-
- Published online by Cambridge University Press:
- 22 January 2016, p. 205
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 20 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 20 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 the Z-module of integral vectors of dimension
the Z-module of integral vectors of dimension  and
and 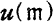
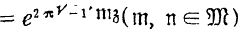 the fundamental theta function
the fundamental theta function 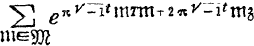 is expressed in the form:
is expressed in the form: 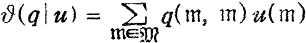 as a series in
as a series in 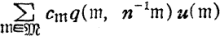 as series of
as series of 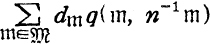 as series in
as series in 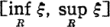 und
und 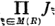 . Laut der Definition von
. Laut der Definition von 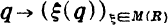 von
von 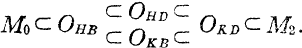
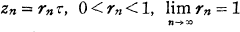 . The non-Euclidean (hyperbolic) distance
. The non-Euclidean (hyperbolic) distance