Published online by Cambridge University Press: 22 January 2016
Let f(z) be a holomorphic function defined in the unit disk |z|<1, which we shall denote by D. Let Σ be a subset of D, whose closure has at least one point in common with C, the circumference of the unit disk. The set of all values a such that the equation f(z) = a has infinitely many solutions in Σ is called the range of f(z) in Σ, and is denoted by R(f, Σ). Let τ be a point of C, and let {zn) be a sequence of points in D with the properties: 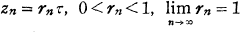 . The non-Euclidean (hyperbolic) distance ρ(zn, zn+1) between two points zn and zn+1 of the sequence is defined to be equal to
. The non-Euclidean (hyperbolic) distance ρ(zn, zn+1) between two points zn and zn+1 of the sequence is defined to be equal to
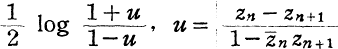
(cf.[3], Ch. II).