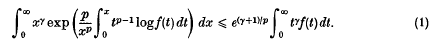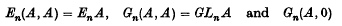Research Article
A note on trigonometric sums in several variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-193
-
- Article
- Export citation
Analytic sets from the point of view of compact sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
On square values of quadratics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-383
-
- Article
- Export citation
On the quantificational logic of intuitionistic set theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-10
-
- Article
- Export citation
Some theorems in the metric theory of diophantine approximation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-394
-
- Article
- Export citation
Perfect powers in values of certain polynomials at integer points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-207
-
- Article
- Export citation
Fourier coefficients of Eisenstein series on non-congruence subgroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-17
-
- Article
- Export citation
Extensions of pro-p groups of cohomological dimension two
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-211
-
- Article
- Export citation
Inequalities related to those of Hardy and of Cochran and Lee
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 395-408
-
- Article
- Export citation
Real forms of cusp singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-232
-
- Article
- Export citation
A sequence well distributed in the square
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-22
-
- Article
- Export citation
Norm form equations. III: positive characteristic
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 409-423
-
- Article
- Export citation
The subnormal structure of general linear groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-431
-
- Article
- Export citation
Some combinatorial results involving shifted Young diagrams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-31
-
- Article
- Export citation
Inequivalent, bordant group actions on a surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-238
-
- Article
- Export citation
An infinite family of non-Haken hyperbolic 3-manifolds with vanishing Whitehead groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-246
-
- Article
- Export citation
The word problem for one-relator semigroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-44
-
- Article
- Export citation
Some one-relator semigroup presentations with solvable word problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-434
-
- Article
- Export citation
Threading knot diagrams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 247-260
-
- Article
- Export citation
On the radical of semigroup algebras satisfying polynomial identities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-50
-
- Article
- Export citation

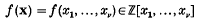
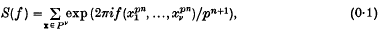
 if, for every compact
if, for every compact  sets (that is, analytic sets), this consistency question is due to Fremlin (see [7], page 483, problem 18). Kunen and Miller [3] have proved the following two theorems.
sets (that is, analytic sets), this consistency question is due to Fremlin (see [7], page 483, problem 18). Kunen and Miller [3] have proved the following two theorems.