Published online by Cambridge University Press: 24 October 2008
An excellent introduction to the metric theory of diophantine approximation is provided by [19], where, in chapter 1·7, the reader may find a discussion of the first two problems considered in this paper. Our initial question concerns the number of solutions of the inequality
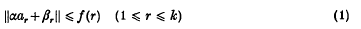
for almost all α(in the sense of Lebesgue measure on ℝ). Here ∥ ∥ denotes distance to a nearest integer, {βr}, {ar} are given sequences of reals and distinct integers respectively, and f is a function taking values in [0, ½] and with Σf(r) divergent (for convenience we write ℱ for the set of all such functions). It is reasonable to expect that, for almost all α and with some additional constraint on f, the number of solutions of (1) is asymptotically equal to

as k tends to infinity.