Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T14:26:05.146Z Has data issue: false hasContentIssue false
  • English
  • Français

Norm form equations. III: positive characteristic

Published online by Cambridge University Press:  24 October 2008

R. C. Mason
R. C. Mason
Affiliation:
Gonville and Caius College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

This paper aims to provide a complete resolution of the general norm form equation over function fields of positive characteristic. In a previous paper [4] we studied norm forms in the simpler case of zero characteristic; that study forms the starting point for the present investigations. Diophantine problems over function fields of positive characteristic were first investigated by Armitage in 1968 [1], who clamied to have established an analogue of the Thue–Siegel–Roth–Uchiyama theorem for such fields. This claim was refuted by Osgood in 1975 [6], who also derived a correct analogue of Thue's approximation theorem. in 1983 a different attack was made on Diophantine problems over function fields, the principal weapon being a bound [2] for the heights of the solutions of the unit equation

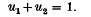
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 3 , May 1986 , pp. 409 - 423
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Armitage, J. V.. The Thue-Siegel-Roth theorem in characteristic p. J. Algebra 9 (1968), 183–189.CrossRefGoogle Scholar
[2]Mason, R. C.. The hyperelliptic equation over function fields. Math. Proc. Cambridge Philos. Soc. 93 (1983), 219–230.CrossRefGoogle Scholar
[3]Mason, R. C.. Diophantine Equations over Function Fields. London Math. Soc. Lecture Notes 96 (Cambridge University Press, 1984).CrossRefGoogle Scholar
[4]Mason, R. C.. Norm form equations I. J. Number Theory (in the Press).Google Scholar
[5]Mason, R. C.. Norm form equations II: decomposable forms (in the Press).Google Scholar
[6]Osgood, C. F.. Effective bounds on the ‘Diophantine approximation’ of algebraic functions over fields of arbitrary characteristic and applications to differential equations. Indag. Math. 37 (1975), no. 2, 105–119.CrossRefGoogle Scholar
[7]Schmidt, W. M.. Norm form equations. Ann. Math. 96 (1972), 526–661.Google Scholar
[8]Brownawell, W. D. and Masser, D. W.. Vanishing sums in function fields. Math. Proc. Cambridge Philos. Soc. 100 (1986) (in the Press).Google Scholar