Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T14:42:43.332Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on trigonometric sums in several variables

Published online by Cambridge University Press:  24 October 2008

R. W. K. Odoni
R. W. K. Odoni
Affiliation:
Department of Mathematics, University of Exeter
Get access Rights & Permissions [Opens in a new window]

Extract

In [3, 4] we showed how the use of a random-walk analogue can be made to yield non-trivial information about the behaviour of certain trigonometric sums in one variable. Our aim here is to show how our method can be adapted to yield similar results for a broad class of trigonometric sums in several variables. Let

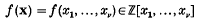
be a polynomial in v independent variables with integral coefficients. We choose integers n ≥ 0, d ≥ 1 and p ≥ 2 with p prime, and assume that f(x) has total degree ≤ d + 1. We shall consider the problem of obtaining non-trivial upper bounds for the absolute value of sums of the type

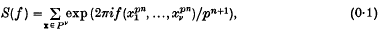
where P = {1, 2, …, p} and f is non-constant.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 2 , March 1986 , pp. 189 - 193
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Deligne, P.. La conjecture de Weil - I. I.H.E.S. Publ. Math. 43 (1974), 273–307.CrossRefGoogle Scholar
[2]Lang, S. and Weil, A.. Number of points of varieties in finite fields. Amer. J. Math. 76 (1954), 819–827.CrossRefGoogle Scholar
[3]Odoni, R. W. K.. The statistics of Weil's trigonometric sums. Math. Proc. Cambridge Philos. Soc. 74 (1973), 467–471.CrossRefGoogle Scholar
[4]Odoni, R. W. K.. Trigonometric sums of Heilbronn's type, Math. Proc. Cambridge Philos. Soc. 98 (1985), 389–396.CrossRefGoogle Scholar
[5]Weil, A.. On some exponential sums. Proc. Nat. Acad. Sci. U.S.A. 34 (1948), 204–207.CrossRefGoogle ScholarPubMed