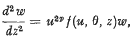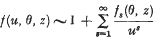Research Article
Polynomial solutions of binomial congruences
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-280
-
- Article
-
- You have access
- Export citation
Mahler's matrices
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-395
-
- Article
-
- You have access
- Export citation
On random interpolation
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-133
-
- Article
-
- You have access
- Export citation
Presidental Address
The pathology of differential equations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-16
-
- Article
-
- You have access
- Export citation
Research Article
Hilbert spaces of generalized functions extending L2, (I)
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-298
-
- Article
-
- You have access
- Export citation
Scales of functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 396-418
-
- Article
-
- You have access
- Export citation
Continuously infinite matrices and the algebraic theory of Fredholm's equation
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
-
- Article
-
- You have access
- Export citation
Criteria for extreme forms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-20
-
- Article
-
- You have access
- Export citation
Measurability of functions of two variables
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-26
-
- Article
-
- You have access
- Export citation
The existence of parametric surface integrals
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-427
-
- Article
-
- You have access
- Export citation
Permutational products of groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-310
-
- Article
-
- You have access
- Export citation
Über die Normalstruktur von mehrfach faktorisierten Gruppen
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-146
-
- Article
-
- You have access
- Export citation
On the spaces of certain classes of entire functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 147-170
-
- Article
-
- You have access
- Export citation
Discontinuous solutions of variational problems
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-37
-
- Article
-
- You have access
- Export citation
The expansion of functions in ultraspherical polynomials
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 428-438
-
- Article
-
- You have access
- Export citation
Desargues' theorem in n-space
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 311-318
-
- Article
-
- You have access
- Export citation
Conditionally convergent spectral expansions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 319-333
-
- Article
-
- You have access
- Export citation
An n-dimensional analogue of Cauchy's integral theorem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-202
-
- Article
-
- You have access
- Export citation
The generation by two operators of the symplectic group over GF(2)*
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 38-46
-
- Article
-
- You have access
- Export citation
Asymptotic formulae for solutions of linear second-order differential equations with a large parameter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 439-464
-
- Article
-
- You have access
- Export citation

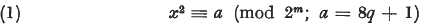
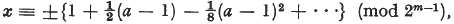
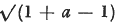 as far as the term of degree
as far as the term of degree 

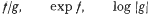

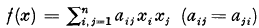 , of determinant
, of determinant 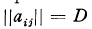 and minimum M for integral
and minimum M for integral 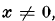 , is said to be extreme if the ratio
, is said to be extreme if the ratio 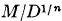 is a (local) maximum for small variations in the coefficients
is a (local) maximum for small variations in the coefficients 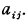 .
.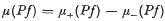
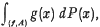
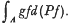
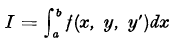
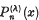 (
(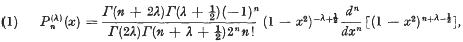
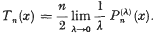
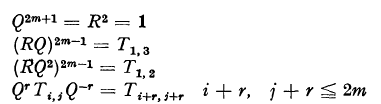
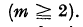 .
.