The most elementary problem of the calculus of variations consists in finding a single-valued function y(x), defined over an interval [a, b] and taking given values at the end points, such that the integral 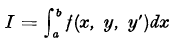is stationary relative to all small weak variations of the function y(x) consistent with the boundary conditions. Since y′ occurs in the integrand, it is clear that I is only defined when y(x) is differentiable and accordingly when y(x) is continuous. Usually y′(x) is also continuous. Occasionally, however, the boundary conditions can only be satisfied and a stationary value of I found, by permitting y′ (x) to be discontinuous at a finite number of points. The arc y = y(x) will then possess ‘corners’ and the well-known Weierstrass-Erdmann corner conditions [1]must be satisfied at all such points by any function y (x) for which I is stationary. Arcs y = y (x) for which y′(x) is continuous except at a finite number of points, are referred to as admissible arcs. In this paper, we shall extend the range of admissible arcs to include those for which y(x) is discontinuous at a finite number of points.