No CrossRef data available.
Article contents
The existence of parametric surface integrals
Published online by Cambridge University Press: 09 April 2009
Extract
In [2] we studied parametric n-surfaces (f, Mn), where Mn was a compact, oriented, topological n-manifold and f a continuous mapping of Mn into the real euclidean k-space Rn (k≧n). A definition of bounded variation was given and, for each surface with bounded variation and each projection P from Rk to Rn, a signed measure: 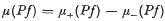 Was constructed. This measure was used to define a linear type of surface integral:
Was constructed. This measure was used to define a linear type of surface integral: 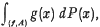 over a “measurable” subset A of Mn, as the Lebesgue-Stieltjes integral:
over a “measurable” subset A of Mn, as the Lebesgue-Stieltjes integral: 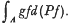 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1960


