No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
Polynomial solutions of a few binomial congruences have been known for a long time. For instance Legendre showed that the congruence 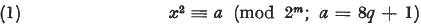 has a solution
has a solution 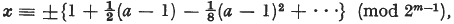 this being the expansion of
this being the expansion of 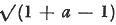 as far as the term of degree m — 3. [1] It seems that only restricted types, e.g. (1), have been investigated.
as far as the term of degree m — 3. [1] It seems that only restricted types, e.g. (1), have been investigated.
 where
where