Research Article
Distribution of unitarily k-free integers
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-141
-
- Article
-
- You have access
- Export citation
Product structure in topological algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-393
-
- Article
-
- You have access
- Export citation
An axially symmetric forced convection problem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-17
-
- Article
-
- You have access
- Export citation
Semirings with a completely simple additive semigroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-267
-
- Article
-
- You have access
- Export citation
Approximation with norms defined by derivations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-24
-
- Article
-
- You have access
- Export citation
Left invariant measure in topological semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 142-145
-
- Article
-
- You have access
- Export citation
On tensor product graphs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 268-273
-
- Article
-
- You have access
- Export citation
Quasi-Frobenius quotient rings of group rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 394-397
-
- Article
-
- You have access
- Export citation
Multiple points and Wallman compactifications
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 274-280
-
- Article
-
- You have access
- Export citation
Intersections of α-spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 398-418
-
- Article
-
- You have access
- Export citation
Recursive density types and Nerode extensions of arithmetic
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-158
-
- Article
-
- You have access
- Export citation
Locally defined Fitting classes
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-32
-
- Article
-
- You have access
- Export citation
Dispersive and explosive mappings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-37
-
- Article
-
- You have access
- Export citation
Generalized discrete l-groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-289
-
- Article
-
- You have access
- Export citation
Semi-stable and stable cacti
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-430
-
- Article
-
- You have access
- Export citation
Generators of reflexive algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-164
-
- Article
-
- You have access
- Export citation
A multifunction generalization of Gale's Ascoli theorem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-171
-
- Article
-
- You have access
- Export citation
Generalized mean value theorems of the differential calculus
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-300
-
- Article
-
- You have access
- Export citation
Stieltjes-type integrals
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 431-448
-
- Article
-
- You have access
- Export citation
On the set of finite subsets of a set
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 38-45
-
- Article
-
- You have access
- Export citation

 be an infinite r.e. repère,
be an infinite r.e. repère, 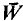 an infinite dimensional r.e. space such that
an infinite dimensional r.e. space such that 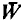 ≦
≦ 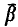 ). A condition is derived that is both necessary and sufficient for the existence of an infinite subset β ⊂
). A condition is derived that is both necessary and sufficient for the existence of an infinite subset β ⊂ 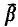 such that
such that 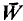 is not an α-space. Examples which satisfy this condition are exhibited, proving that the class of α-spaces is not closed under intersections.
is not an α-space. Examples which satisfy this condition are exhibited, proving that the class of α-spaces is not closed under intersections.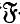 -injectors”, for
-injectors”, for 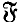 a Fitting class. In general the behaviour of Fitting classes and injectors seems somewhat mysterious and hard to determine. This is in contrast to the situation for saturated formations and
a Fitting class. In general the behaviour of Fitting classes and injectors seems somewhat mysterious and hard to determine. This is in contrast to the situation for saturated formations and 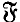 -projectors of finite solvable groups which, because of the equivalence saturated formations and locally defined formations, can be studied in a much more detailed way. However for those Fitting classes
-projectors of finite solvable groups which, because of the equivalence saturated formations and locally defined formations, can be studied in a much more detailed way. However for those Fitting classes 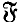 that are “locally defined” the theory of
that are “locally defined” the theory of 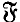 -injectors can be made more explicit by considering various centralizers involving the local definition of
-injectors can be made more explicit by considering various centralizers involving the local definition of 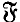 , giving results analogous to some of those concerning locally defined formations. Particular attention will be given to the subgroup B(
, giving results analogous to some of those concerning locally defined formations. Particular attention will be given to the subgroup B(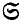 ) defined by
) defined by 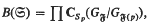
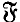 (
(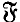 , and the
, and the 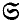 −
− 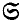 ) plays a role very much like that of Graddon's
) plays a role very much like that of Graddon's 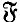 -reducer in Graddon (1971). An
-reducer in Graddon (1971). An 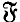 -injector of
-injector of 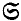 ) is an
) is an 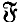 -injector of
-injector of 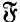
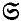 ) is an
) is an 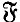 -injector of
-injector of 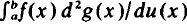 in Russell (1970). He showed that the two integrals are not equivalent.
in Russell (1970). He showed that the two integrals are not equivalent.