Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T23:22:46.160Z Has data issue: false hasContentIssue false
  • English
  • Français

Intersections of α-spaces

Published online by Cambridge University Press:  09 April 2009

Northrup Fowler III
Northrup Fowler III
Affiliation:
Hamilton CollegeClinton, New York 13323, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 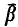be an infinite r.e. repère, 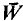an infinite dimensional r.e. space such that 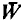≦ L(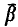). A condition is derived that is both necessary and sufficient for the existence of an infinite subset β ⊂ 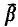such that L(β)∪ 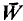is not an α-space. Examples which satisfy this condition are exhibited, proving that the class of α-spaces is not closed under intersections.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 20 , Issue 4 , November 1975 , pp. 398 - 418
Copyright
Copyright © Australian Mathematical Society 1975

References

Dekker, J. C. E. (1969), ‘Countable Vector Spaces with Recursive Operations, Part I’, The Journal of Symbolic Logic 34, 363–387.CrossRefGoogle Scholar
Dekker, J. C. E. (1971), ‘Countable Vector Spaces with Recursive Operations, Part II’, J. Symbolic Logic 36, 477–493.CrossRefGoogle Scholar
Fowler, N. (to appear), ‘agr;-Decompositions of agr;-Spaces’.Google Scholar
Guhl, R. (to appear), ‘A Theorem on Recursively Enumerable Vector Spaces’, Notre Dame Joural of Formal Logic.Google Scholar
Soare, R. I. (1974), ‘Isomorphism on Countable Vector Spaces with Recursive Operations’, J. Austral Math. Soc. 18, 230–235.CrossRefGoogle Scholar