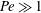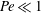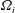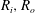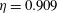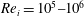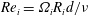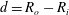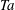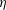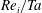JFM Papers
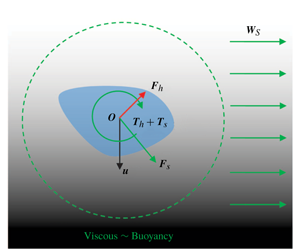
Motion of an arbitrarily shaped particle in a density stratified fluid
-
- Published online by Cambridge University Press:
- 13 March 2020, A16
-
- Article
- Export citation
Large-eddy simulation and modelling of Taylor–Couette flow
-
- Published online by Cambridge University Press:
- 12 March 2020, A17
-
- Article
- Export citation
Gravity–capillary waves in reduced models for wave–structure interactions
-
- Published online by Cambridge University Press:
- 13 March 2020, A18
-
- Article
- Export citation
Friction properties of superhydrophobic ridges
-
- Published online by Cambridge University Press:
- 13 March 2020, A19
-
- Article
- Export citation
Electrostatic forcing of thin leaky dielectric films under periodic and steady fields
-
- Published online by Cambridge University Press:
- 13 March 2020, A20
-
- Article
- Export citation
Pulsating spiral Poiseuille flow
-
- Published online by Cambridge University Press:
- 17 March 2020, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An inviscid analysis of swept oblique shock reflections
-
- Published online by Cambridge University Press:
- 17 March 2020, A22
-
- Article
- Export citation
Tri-periodic fully three-dimensional analytic solutions for the Navier–Stokes equations
-
- Published online by Cambridge University Press:
- 17 March 2020, A23
-
- Article
- Export citation
Erratum
Modelling film flows down a fibre – ERRATUM
-
- Published online by Cambridge University Press:
- 17 March 2020, E1
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum
Structural and stability characteristics of jets in crossflow – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 20 March 2020, E2
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 890 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 March 2020, p. f1
-
- Article
-
- You have access
- Export citation