Published online by Cambridge University Press: 13 March 2020
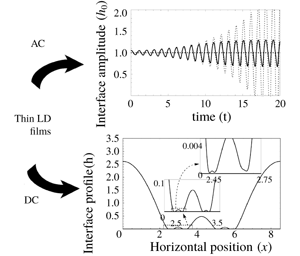
The linear and nonlinear dynamics of an interface separating a thin liquid film and a hydrodynamically passive ambient medium, subject to normal electrostatic forcing, are investigated. A reduced-order model is developed for the case where both fluids are taken to be leaky dielectrics (LD). Cases of time periodic as well as steady forcing are studied. In the former case, an important result is the elucidation of two forms of resonant instability than can occur in LD films. These correspond to an inertial resonance due to mechanical inertia of the fluid and an inertialess resonance due to charge capacitance at the interface that is similar to mechanically forced films with an insoluble surfactant. In the case of steady forcing, the long-time dynamics exhibits spontaneous sliding as the interface approaches the wall, for the two limiting cases of a perfect conductor–perfect dielectric pair as well as a pair of perfect dielectrics. Under these limits, only the normal component of the Maxwell stress at the interface is significant and the interface dynamics resembles that of a Rayleigh–Taylor unstable interface. For a general pair of leaky dielectrics studied in the limit of fast relaxation times, the presence of interfacial charge prevents the onset of sliding. For the special case when the square of the conductivity ratio equals the permittivity ratio, the interface exhibits cascading structures, similar to those reported for the long-wave Marangoni instability.
Spatio-temporal evolution of subharmonic (SH) and harmonic (H) Faraday instability, exhibited by a pair of perfect dielectrics. Properties of silicone oil and air in table 1 are used for simulations. SH response corresponds to k=0.23, A=10.7kV and H response corresponds to k=0.42, A=13.1kV.
Evolution of interface between thin leaky dielectric films with σ=ε, exhibiting spontaneous sliding. This case corresponds to the condition of zero tangential stress. Similarly, sliding is also observed in the case of a pair of perfect dielectrics as well as a perfect conductor-perfect dielectric pair, where too the interface is solely under the influence of normal stress.
Long-time cascading structures exhibited by the interface between a pair of leaky dielectrics for the case of zero normal stress (i.e. σ=ε1/2). The interface evolution is due to the tangential component of Maxwell stress and undergoes a series of buckling events as it approaches the wall.