Transition control by suction in a three-dimensional boundary-layer flow subject to cross-flow instability is investigated using direct numerical simulation. Whereas the classical application of (homogeneous) suction at the wall is aimed at modifying the quasi-two-dimensional base flow to weaken primary cross-flow instability, here the three-dimensional nonlinear disturbance state with large-amplitude steady cross-flow vortices (CFVs) is controlled. Strong, localized ‘pinpoint’ suction is shown to be suitable for altering the CFVs and the associated flow field such that secondary instability is weakened or even completely suppressed. Thus significant delay of transition to turbulence can be achieved.

We study the fluid dynamics of rolling wheels at Reynolds number 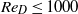(where 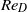is the Reynolds number based on the wheel diameter), with the objective of characterizing the various regimes of steady and unsteady motion. Regardless of the Reynolds number, the flow is found to separate approximately 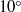upstream of the apex of the wheel, where a saddle point in the pseudo-streamtrace pattern is observed. Under the flow conditions here essayed, the drag coefficient steadily decreases with , and the lift coefficient remains strictly positive. The positive lift provided by the rolling wheel is associated with the presence of a strong (positive) peak of the static pressure in the upstream proximity of the contact point with the ground, which we interpret as the result of the impingement of flow particles entrained in the boundary layer that develops on the front part of the wheel. Steady laminar flow is observed up to , which is characterized by a three-dimensional wake whose length increases with the Reynolds number. Unsteadiness is first observed at 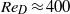, under which conditions the flow retains planar symmetry, and is characterized by the quasi-periodic shedding of hairpin vortices. Transition to three-dimensional flow happens at 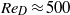, in which case a sinuous mode of instability in the wheel wake is established, which modulates the shedding of the hairpins, and which causes the onset of a non-zero side force. At the highest Reynolds number considered here (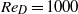) the wake exhibits some characters of turbulence, with wide-band frequency spectra, and its topology entirely changes, becoming split into two parts, and being much shortened compared to the lower- 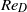cases. Despite the limitation of the study to low Reynolds numbers we find that, once significant three-dimensionality and scale separation are established in the wheel wake, the nature of the flow becomes qualitatively similar to fully developed turbulent flow. In perspective, this observation opens interesting avenues for the prediction of unsteady flow around rotating tyres at moderate computational cost.

Homogeneous condensation of vapours mixed with a carrier gas in the stagnation point boundary layer flow near a cold wall is considered. There is a condensation region near the wall with supersaturated vapour. Assuming that the surface tension times the molecular area is much larger than the thermal energy far from the wall, droplets are nucleated exclusively in a narrow nucleation layer where the Zeldovich flux of clusters surpassing the critical nucleus size is at a maximum. The vapour condenses in the free molecular regime on the droplets, which are thermophoretically attracted to the wall. Unlike the narrow condensation region for heterogeneous condensation on solid particles, in the case of homogeneous condensation the condensation region is wide even when the rate of vapour scavenging by droplets is large. A singular perturbation theory of homogeneous vapour condensation in boundary layer flow approximates very well the vapour and droplet density profiles, the nucleation layer and the deposition rates at the wall for wide ranges of the wall temperature and the scavenging parameter . A key point in the theory is to select a trial vapour number density profile among a one parameter family of profiles between an upper and a lower bound. The maximum of the Zeldovich flux for supercritical nuclei provides the approximate location of the nucleation layer and an approximate droplet density profile. Then the condensate number of molecules and the vapour density profile are calculated by matched asymptotic expansions that also yield the deposition rates. For sufficiently large wall temperatures, a more precise corrected asymptotic theory is given.

We use ultra-high-speed video imaging to observe directly the earliest onset of prompt splashing when a drop impacts onto a smooth solid surface. We capture the start of the ejecta sheet travelling along the solid substrate and show how it breaks up immediately upon emergence from the underneath the drop. The resulting micro-droplets are much smaller and faster than previously reported and may have gone unobserved owing to their very small size and rapid ejection velocities, which approach 100 m s−1, for typical impact conditions of large rain drops. We propose a phenomenological mechanism which predicts the velocity and size distribution of the resulting microdroplets. We also observe azimuthal undulations which may help promote the earliest breakup of the ejecta. This instability occurs in the cusp in the free surface where the drop surface meets the radially ejected liquid sheet.

We present experimental and computational studies of the propagation of internal waves in a stratified fluid with an exponential density profile that models the deep ocean. The buoyancy frequency profile (proportional to the square root of the density gradient) varies smoothly by more than an order of magnitude over the fluid depth, as is common in the deep ocean. The non-uniform stratification is characterized by a turning depth , where is equal to the wave frequency and . Internal waves reflect from the turning depth and become evanescent below the turning depth. The energy flux below the turning depth is shown to decay exponentially with a decay constant given by , which is the horizontal wavenumber at the turning depth. The viscous decay of the vertical velocity amplitude of the incoming and reflected waves above the turning depth agree within a few per cent with a previously untested theory for a fluid of arbitrary stratification (Kistovich and Chashechkin, J. Appl. Mech. Tech. Phys., vol. 39, 1998, pp. 729–737).

Results are presented from a direct numerical simulation of a particle-laden spatially developing turbulent boundary layer up to . The peculiar feature of a boundary-layer flow seeded with heavy particles is the variation of the local dimensionless parameters defining the fluid–particle interactions along the streamwise direction. Two different Stokes numbers can be defined, one using inner flow units and the other with outer units. Since these two Stokes numbers exhibit different decay rates in the streamwise direction, we find a decoupled particle dynamics between the inner and the outer region of the boundary layer. Preferential near-wall particle accumulation is similar to that observed in turbulent channel flow, while different behaviour characterizes the outer region. Here the concentration and the streamwise velocity profiles are found to be self-similar and to depend only on the local value of the outer Stokes number and the rescaled wall-normal distance. These new results are powerful in view of engineering and environmental applications and corresponding flow modelling.

We investigate laminar boundary-layer flows due to translating, stretching, incompressible sheets. Unlike the classical problem in the literature where the mechanics of the sheet are neglected, and kinematics are prescribed, the dynamics of both the fluid and the sheet are herein coupled. Two types of stretching sheets are considered: an elastic sheet that obeys linear elasticity and a sheet that deforms as a viscous Newtonian fluid. In both cases, we find self-similar solutions to the coupled fluid/sheet system. These self-similar solutions are only valid under limiting conditions.