Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T16:52:33.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similar transport of inertial particles in a turbulent boundary layer

Published online by Cambridge University Press:  13 July 2012

G. Sardina ,
P. Schlatter ,
F. Picano ,
C. M. Casciola ,
L. Brandt  and
D. S. Henningson
G. Sardina*
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden Facoltà di Ingegneria, Architettura e Scienze Motorie, UKE–Università Kore di Enna, 94100 Enna, Italy
P. Schlatter
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
F. Picano
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza University of Rome, 00184 Rome, Italy
C. M. Casciola
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza University of Rome, 00184 Rome, Italy
L. Brandt
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
D. S. Henningson
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

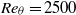Results are presented from a direct numerical simulation of a particle-laden spatially developing turbulent boundary layer up to . The peculiar feature of a boundary-layer flow seeded with heavy particles is the variation of the local dimensionless parameters defining the fluid–particle interactions along the streamwise direction. Two different Stokes numbers can be defined, one using inner flow units and the other with outer units. Since these two Stokes numbers exhibit different decay rates in the streamwise direction, we find a decoupled particle dynamics between the inner and the outer region of the boundary layer. Preferential near-wall particle accumulation is similar to that observed in turbulent channel flow, while different behaviour characterizes the outer region. Here the concentration and the streamwise velocity profiles are found to be self-similar and to depend only on the local value of the outer Stokes number and the rescaled wall-normal distance. These new results are powerful in view of engineering and environmental applications and corresponding flow modelling.

JFM classification

Boundary Layers: Boundary Layers Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 584 - 596
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 447–464.CrossRefGoogle Scholar
2. Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550 (1), 349–358.CrossRefGoogle Scholar
3. Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32 (3), 565–568.2.0.CO;2>CrossRefGoogle Scholar
4. Chamecki, M. & Meneveau, C. 2011 Particle boundary layer above and downstream of an area source: scaling, simulations, and pollen transport. J. Fluid Mech. 683 (1), 1–26.Google Scholar
5. Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S. 2007 SIMSON: A pseudo-spectral solver for incompressible boundary layer flows. Tech. Rep. TRITA-MEK 2007:07, KTH Mechanics.Google Scholar
6. Ferrante, A. & Elghobashi, S. E. 2007 Reynolds number effect on drag reduction in a bubble-laden spatially developing turbulent boundary layer. J. Fluid Mech. 572, 145–177.CrossRefGoogle Scholar
7. Gerashchenko, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617 (1), 255–281.Google Scholar
8. Grindle, T. J., Burcham, F. W. & Hugh, L. 2003Engine damage to a NASA DC-8-72 airplane from a high-altitude encounter with a diffuse volcanic ash cloud. NASA/TM-2003-212030.Google Scholar
9. Kaftori, D., Hetsroni, G. & Banerjee, S. 1995a Particle behaviour in the turbulent boundary layer. Part 1. Motion, deposition, and entrainment. Phys. Fluids 7 (5), 1095–1106.Google Scholar
10. Kaftori, D., Hetsroni, G. & Banerjee, S. 1995b Particle behaviour in the turbulent boundary layer. Part 2. Velocity and distribution profiles. Phys. Fluids 7, 1107.Google Scholar
11. Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
12. Mattson, M. & Mahesh, K. 2011 Simulation of bubble migration in a turbulent boundary layer. Phys. Fluids 23, 045107.Google Scholar
13. Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a non-uniform flow. Phys. Fluids 26, 883.CrossRefGoogle Scholar
14. Messeguer, J. 2003 Gene flow assessment in transgenic plants. Plant Cell, Tissue and Organ Culture 73 (3), 201–212.Google Scholar
15. O’Connell, L. M., Mosseler, A. & Rajora, O. P. 2007 Extensive long-distance pollen dispersal in a fragmented landscape maintains genetic diversity in white spruce. J. Heredity 98 (7), 640.CrossRefGoogle Scholar
16. Picano, F., Battista, F., Troiani, G. & Casciola, C. M. 2011 Dynamics of PIV seeding particles in turbulent premixed flames. Exp. Fluids 50 (1), 75–88.Google Scholar
17. Picano, F., Sardina, G. & Casciola, C. M. 2009 Spatial development of particle-laden turbulent pipe flow. Phys. Fluids 21, 093305.CrossRefGoogle Scholar
18. Picano, F., Sardina, G., Gualtieri, P. & Casciola, C. M. 2010 Anomalous memory effects on transport of inertial particles in turbulent jets. Phys. Fluids 22, 051705.Google Scholar
19. Righetti, M. & Romano, G. P. 2004 Particle–fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 505, 93–121.Google Scholar
20. Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.Google Scholar
21. Sardina, G., Picano, F., Schlatter, P., Brandt, L. & Casciola, C. M. 2011 Large scale accumulation patterns of inertial particles in wall-bounded turbulent flow. Flow Turbul. Combust. 86, 519–532.CrossRefGoogle Scholar
22. Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.CrossRefGoogle Scholar
23. Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
24. Schlatter, P., Örlü, R., Li, Q., Brethouwer, G., Fransson, J. H. M., Johansson, A. V., Alfredsson, P. H. & Henningson, D. S. 2009 Turbulent boundary layers up to studied through numerical simulation and experiments. Phys. Fluids 21, 051702.CrossRefGoogle Scholar
25. Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar