Recent theoretical progress using multiscale asymptotic analysis has revealed various possible regimes of stratified turbulence. Notably, buoyancy transport can either be dominated by advection or diffusion, depending on the effective Péclet number of the flow. Two types of asymptotic models have been proposed, which yield measurably different predictions for the characteristic vertical velocity and length scale of the turbulent eddies in both diffusive and non-diffusive regimes. The first, termed a ‘single-scale model’, is designed to describe flow structures having large horizontal and small vertical scales, while the second, termed a ‘multiscale model’, additionally incorporates flow features with small horizontal scales, and reduces to the single-scale model in their absence. By comparing predicted vertical velocity scaling laws with direct numerical simulation data, we show that the multiscale model correctly captures the properties of strongly stratified turbulence within regions dominated by small-scale isotropic motions, whose volume fraction decreases as the stratification increases. Meanwhile its single-scale reduction accurately describes the more orderly, layer-like, quiescent flow outside those regions.

The nonlinear dynamics of a helical vortex disturbed by a long-wave-instability mode is studied by direct numerical simulation. Vortex reconnection or self-reconnection of the helical vortex is shown to play a crucial role depending on the pitch of the helical vortex. For the larger pitch, a vortex ring is created after the vortex reconnection; it detaches from the remaining helical vortex, whose pitch is doubled. A vortex ring is also created for the smaller pitch; however, it forms a linked system with the remaining vortex. The topological constraint due to this linkage forces strong interaction between the different parts of the helical vortex, leading to turbulent transition.

Direct numerical simulations (DNS) were carried out to investigate flow control for transition delay using steady blowing/suction strips at the wall of a flared cone at Mach 6 and zero angle of attack. For the numerical investigations of the transition control strategy, the flared cone geometry and the flow conditions of the experiments in the Boeing/Air Force Office of Scientific Research (AFOSR) Mach 6 Quiet Tunnel (BAM6QT) at Purdue University were chosen. For the DNS, transition was initiated by introducing random disturbances at the inflow of the computational domain, emulating ‘natural’ transition in wind-tunnel experiments caused by free-stream noise. In both wind-tunnel experiments and numerical simulations, streamwise ‘hot’ streaks were found on the surface of the flared cone, which are caused by a nonlinear interaction of an axisymmetric second-mode wave and a pair of oblique waves of the same frequency (‘fundamental resonance’). The objective of the flow control strategy proposed here is to delay the transition onset, and thus mitigate the negative consequences associated with the nonlinear transition stages, i.e. the development of hot streaks and large wall-pressure amplitudes that were observed in experiments and DNS. Our previous so-called ‘controlled’ transition simulations have shown that flow control using steady blowing and suction strips can lead to a significant delay of the hot streak development on the surface of the flared cone. The simulation results presented in this paper show that this flow control strategy remains effective, even in a natural transition scenario characterized by broadband disturbances.

Different types of neural networks have been used to solve the flow sensing problem in turbulent flows, namely to estimate velocity in wall-parallel planes from wall measurements. Generative adversarial networks (GANs) are among the most promising methodologies, due to their more accurate estimations and better perceptual quality. This work tackles this flow sensing problem in the vicinity of the wall, addressing for the first time the reconstruction of the entire three-dimensional (3-D) field with a single network, i.e. a 3-D GAN. With this methodology, a single training and prediction process overcomes the limitation presented by the former approaches based on the independent estimation of wall-parallel planes. The network is capable of estimating the 3-D flow field with a level of error at each wall-normal distance comparable to that reported from wall-parallel plane estimations and at a lower training cost in terms of computational resources. The direct full 3-D reconstruction also unveils a direct interpretation in terms of coherent structures. It is shown that the accuracy of the network depends directly on the wall footprint of each individual turbulent structure. It is observed that wall-attached structures are predicted more accurately than wall-detached ones, especially at larger distances from the wall. Among wall-attached structures, smaller sweeps are reconstructed better than small ejections, while large ejections are reconstructed better than large sweeps as a consequence of their more intense footprint.

The flow resistance, i.e. friction factor times Reynolds number ($\,f\,{Re}$), of longitudinal-fin heat sinks with or without clearance between a shroud and the tips of the fins is an important parameter in thermal design. This is because it dictates the caloric resistance of the heat sink, i.e. change in bulk temperature of the fluid flowing through it. When there is no clearance and the common and oft-valid assumption of negligible fin thickness is invoked, $f\,{Re}$ corresponds to simply that of a rectangular duct. However, with clearance, only numerical results are available as per the well-known study by Sparrow, Baliga and Patankar (ASME J. Heat Transfer, vol. 100, 1978). We develop analytical formulae for $f\,{Re}$ for fully developed flow with clearance. The exact solution is provided by an integral formula derived via conformal mappings. Additionally, simple formulae are derived via asymptotic expansions in three cases: (1) the fin spacing is small compared to the fin height and clearance; (2) the clearance is small compared to the fin spacing, which is small compared to the fin height; (3) the same as case (2) but valid for larger clearances. The different asymptotic formulae are compared to the exact formula, and together cover almost the entire relevant parameter range (for fin spacing and clearance) with errors of less than 15 %. A formula for the limiting case of no clearance is shown to be more accurate, for any fin spacing, than a widely used correlation from the literature.

Numerous studies have indicated that turbulence typically initiates along the boundary layer of the stationary disk within a rotor–stator cavity. To describe the transition process to turbulence on the stationary side of a closed rotor–stator cavity, a comprehensive approach combining global linear stability analysis with direct numerical simulation was adopted in the present study. The proposed model aligns with that of Yim et al. (J. Fluid Mech., vol. 848, 2018, pp. 631–647), who investigated the stability characteristics of the rotating-disk boundary layer in a rotor–stator cavity. In order to achieve a stable inflow for the stationary-disk boundary layer, we rotate the shroud together with the rotating disk. Through careful global stability analysis, the predominant spiral mode exhibiting the highest instability in the boundary layer of the stationary disk was discerned, corroborating observations from simulations. Initially, the spiral mode undergoes linear amplification, reaches a state of linear saturation and enters the nonlinear regime. Following nonlinear saturation in the flow field, a circular wave mode arises due to the influence of mean flow distortion. As the Reynolds number attained a sufficiently high level, the interplay between the downstream-propagating circular mode and spiral mode amplified disturbances in the boundary layer of the stationary disk, ultimately leading to the development of localised turbulence at the mid-radius of the rotor–stator cavity. Notably, the present study is the first to elucidate the coexistence of laminar–transitional–turbulent flow states in the stationary-disk boundary layer through direct numerical simulations.

We present a theory to describe the Nusselt number, $\operatorname {\mathit {Nu}}$, corresponding to the heat or mass flux, as a function of the Rayleigh–Darcy number, $\operatorname {\mathit {Ra}}$, the ratio of buoyant driving force over diffusive dissipation, in convective porous media flows. First, we derive exact relationships within the system for the kinetic energy and the thermal dissipation rate. Second, by segregating the thermal dissipation rate into contributions from the boundary layer and the bulk, which is inspired by the ideas of the Grossmann and Lohse theory (J. Fluid Mech., vol. 407, 2000; Phys. Rev. Lett., vol. 86, 2001), we derive the scaling relation for $\operatorname {\mathit {Nu}}$ as a function of $\operatorname {\mathit {Ra}}$ and provide a robust theoretical explanation for the empirical relations proposed in previous studies. Specifically, by incorporating the length scale of the flow structure into the theory, we demonstrate why heat or mass transport differs between two-dimensional and three-dimensional porous media convection. Our model is in excellent agreement with the data obtained from numerical simulations, affirming its validity and predictive capabilities.

We optimize jet mixing using large eddy simulations (LES) at a Reynolds number of $3000$. Key methodological enablers consist of Bayesian optimization, a surrogate model enhanced by deep learning and persistent data topology for physical interpretation. The mixing performance is characterized by an equivalent jet radius ($R_{eq}$) derived from the streamwise velocity in a plane located $8$ diameters downstream. The optimization is performed in a 22-dimensional actuation space that comprises most known excitations. This search space parameterizes the distributed actuation imposed on the bulk flow and at the periphery of the nozzle in the streamwise and radial directions. The momentum flux measures the energy input of the actuation. The optimization quadruples the jet radius $R_{eq}$ with a $7$-armed blooming jet after around $570$ evaluations. The control input requires $2\,\%$ momentum flux of the main flow, which is one order of magnitude lower than an ad hoc dual-mode excitation. Intriguingly, a pronounced suboptimum in the search space is associated with a double-helix jet, a new flow pattern. This jet pattern results in a mixing improvement comparable to the blooming jet. A state-of-the-art Bayesian optimization converges towards this double-helix solution. The learning is accelerated and converges to another better optimum by including a deep-learning-enhanced surrogate model trained along the optimization. Persistent data topology extracts the global and many local minima in the actuation space. These minima can be identified with flow patterns beneficial to the mixing.

A distinguishing feature of the bi-stable wake is that the wake persists in either of two preferred states for a sufficiently long time. Aiming to understand the persistence mechanism, this paper numerically investigates the airwake characteristics of the Chalmers ship model (CSM) using large eddy simulation with a wall-adapting local-eddy viscosity model and is complemented by experimental testings for validations. There are two cases of interest: (i) the baseline CSM with a sharp-edged superstructure front that induces massive boundary layer separation; (ii) the front-rounded (FR) CSM with suppressed flow separation. During a characteristic time ($t^*$) of 1142 (26.5 s), the baseline case has a frequently switching wake, whereas the FR wake maintains a stable asymmetric structure with only one switch attempt. To understand the different wake behaviours, the study starts by analysing wake flow structures, vortex cores and the wake dynamics, followed by investigating the instantaneous flow physics. Results suggest that the baseline wake has a weak bi-stable pattern, whereas the FR wake behaves similarly to a reflectional symmetry breaking state of a potential bi-stable wake. The wake switching is found to be driven by the tilting of (vertical-oriented) $z$-vorticity sheets from either side of the base toward the centre. This tilting behaviour is subjected to the high-magnitude vorticity that sheds from the upstream flow separation at the front sharp edges. With the sharp edges rounded in the FR case, the upstream vorticity is mitigated and the tilting effect is significantly reduced, leading to a more stable wake structure. The reasoning provided in the paper potentially explains the persistence mechanism of the bi-stable wake.

Numerical simulations of thermoelectrohydrodynamic convection in a dielectric liquid inside a finite-length cylindrical annulus with a fixed temperature difference have been performed with increasing high-frequency electric tension under microgravity conditions. The electric field, coupled with the permittivity gradient, generates a dielectrophoretic buoyancy force whose non-conservative part can induce thermoelectric convection in the liquid. The liquid remains in a conductive state below a critical value of the applied electric voltage. At a critical value, a supercritical bifurcation occurs from the conductive state to a convective state made of stationary helicoidal vortices. A further increase of electric voltage leads to oscillatory helicoidal vortices and then to wavy patterns before spoke patterns dominate the convective flow. The dielectrophoretic force is shown to enhance the heat transfer from the hot to cold walls due to induced convective flows. Particularly, these results demonstrate that the dielectrophoretic buoyancy force holds promise to replace the gravitational force to induce efficient heat transfer in microgravity conditions, and they contribute to a better fundamental understanding of heat transfer in microgravity.

It is known that the dispersion of colloidal particles in porous media is determined by medium structure, pore-scale flow variability and diffusion. However, much less is known about how diffusiophoresis, that is, the motion of colloidal particles along salt gradients, impacts large-scale particle dispersion in porous media. To shed light on this question, we perform detailed pore-scale simulations of fluid flow, solute transport and diffusiophoretic particle transport in a two-dimensional hyper-uniform porous medium. Particles and solute are initially uniformly distributed throughout the medium. The medium is flushed at constant flow rate, and particle breakthrough curves are recorded at the outlet to assess the macroscopic effects of diffusiophoresis. Particle breakthrough curves show non-Fickian behaviour manifested by strong tailing that is controlled by the diffusiophoretic mobility. Although diffusiophoresis is a short-time, microscopic phenomenon owing to the fast attenuation of salt gradients, it governs macroscopic colloid dispersion through the partitioning of particles into transmitting and dead-end pores. We quantify these behaviours by an upscaled analytical model that describes both the retention and release of colloids in dead-end pores and the observed long-time tailings. Our results suggest that diffusiophoresis is an efficient tool to control particle dispersion and filtration through porous media.

The unsteady mechanism of unstart flow for an inlet with rectangular-to-elliptical shape transition (REST) under the off-design condition at a Mach of 4 is investigated using the delay detached eddy simulation method. With the help of numerical simulations, the unsteady dynamics, especially the low-frequency characteristics of the REST inlet unstart flow, as well as the self-sustaining mechanism, is investigated. The instantaneous flow illustrates the unsteady phenomena of the REST unstart flow, including the interaction between the cowl-closure leading edge (CLE) shock and the shear layer, breathing of the separation bubble, flapping of the separation shock, instability of the shear layer and vortex shedding along the shear layer. The spectral analysis reveals that the lower frequency dynamics is associated with the breathing of the separation bubble and the flapping motion of the separation shock wave, while the higher frequency is related to the instability of the shear layer affected by cowl-closure leading edge shock and the formation of shedding vortices. Further, coherence analysis shows that the contribution of these flow structures dominating the low-frequency dynamics couple with each other. Based on the dynamic mode decomposition results, the characteristics that contribute to the unsteady behaviour of unstart flow are summarized. The streamwise vortices downstream of the separation and the shedding vortices are believed to be the main driving force of the global low-frequency unsteadiness of the REST inlet unstart flow under the off-design condition. Moreover, the CLE shock plays an important role in the process during the dominant flow structure conversion from the backflow within the separation bubble into elongated streamwise structures.

Convolutional autoencoders are used to deconstruct the changing dynamics of two-dimensional Kolmogorov flow as $Re$ is increased from weakly chaotic flow at $Re=40$ to a chaotic state dominated by a domain-filling vortex pair at $Re=400$. ‘Latent Fourier analysis’ (Page et al., Phys. Rev. Fluids 6, 2021, p. 034402) reveals a detached class of bursting dynamics at $Re=40$ which merge with the low-dissipation dynamics as $Re$ is increased to $100$ and provides an efficient representation within which to find unstable periodic orbits (UPOs) using recurrent flow analysis. Focusing on initial guesses with energy in higher latent Fourier wavenumbers allows a significant number of high-dissipation-rate UPOs associated with the bursting events to be found for the first time. At $Re=400$, the UPOs discovered at lower $Re$ move away from the attractor, and an entirely different embedding structure is formed within the network devoid of small-scale vortices. Here latent Fourier projections identify an associated ‘large-scale’ UPO which we believe to be a finite-$Re$ continuation of a solution to the Euler equations.

The low-frequency modal and non-modal linear dynamics of an incompressible, pressure-gradient-induced turbulent separation bubble (TSB) are investigated, with the objective of studying the mechanism responsible for the low-frequency contraction and expansion (breathing) commonly observed in experimental studies. The configuration of interest is a TSB generated on a flat test surface by a succession of adverse and favourable pressure gradients. The base flow selected for the analysis is the average TSB from the direct numerical simulation of Coleman et al. (J. Fluid Mech., vol. 847, 2018, pp. 28–70). Global mode analysis reveals that the eigenmodes of the linear operator are damped for all frequencies and wavenumbers. Furthermore, the least damped eigenmode appears to occur at zero frequency and low, non-zero spanwise wavenumber when scaled with the separation length. Resolvent analysis is then employed to examine the forced dynamics of the flow. At low frequency, a region of low, non-zero spanwise wavenumber is also discernible, where the receptivity appears to be driven by the identified weakly damped global mode. The corresponding optimal energy gain is shown to have the shape of a first-order, low-pass filter with a cut-off frequency consistent with the low-frequency unsteadiness in TSBs. The results from resolvent analysis are compared to the unsteady experimental database of Le Floc'h et al. (J. Fluid Mech., vol. 902, 2020, A13) in a similar TSB flow. The alignment between the optimal response and the first spectral proper orthogonal decomposition mode computed from the experiments is shown to be close to $95\,\%$, while the spanwise wavenumber of the optimal response is consistent with that of the low-frequency breathing motion captured experimentally. This indicates that the fluctuations observed experimentally at low frequency closely match the response computed from resolvent analysis. Based on these results, we propose that the forced dynamics of the flow, driven by the weakly damped global mode, serve as a plausible mechanism for the origin of the low-frequency breathing motion commonly observed in experimental studies of TSBs.

A theory of incompressible turbulent plane jets (TPJs) is proposed by advancing an improved boundary layer approximation over the limiting classical – retaining more terms in the momentum balance equations. A pressure deficit inside the jet (with respect to the ambient) must exist due to transverse turbulence (Miller & Comings, J. Fluid Mech., vol. 3, 1957, pp. 1–16; Hussain & Clarke, Phys. Fluids, vol. 20, 1977, pp. 1416–1426). Contrary to the universally accepted invariance of the total momentum flux 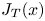$J_T(x)$ (non-dimensionalized by its inlet value) as a function of the streamwise distance 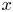$x$, we prove that 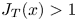$J_T(x) >1$ – a condition that all TPJs must satisfy; surprisingly, prior theories and most experiments do not satisfy this condition. This motivated us to apply Lie symmetry analysis with translational and dilatational transformations of the modified equations (incorporating 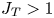$J_T>1$), which yields scaling laws for key jet measures: the mean streamwise and transverse velocities 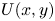$U(x,y)$ and 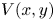$V(x,y)$, the turbulence intensities, the Reynolds shear stress 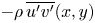$-\rho \,\overline {u'v'}(x,y)$, the mean pressure 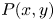$P(x,y)$, etc. Experiments satisfying 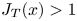$J_T(x)>1$ validate our predictions for all jet measures, including, among others, the profiles of 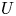$U$, 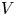$V$ and 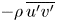$-\rho \,\overline {u'v'}$. We further predict 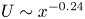$U \sim x^{-0.24}$, 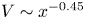$V \sim x^{-0.45}$, 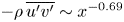$-\rho \,\overline {u'v'}\sim x^{-0.69}$, the mass flux 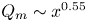$Q_m \sim x^{0.55}$, and 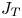$J_T$ increases to approximately 1.5. Contrary to the classical linear jet spread, we find sublinear spread, with the jet half-width growing like 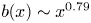$b(x)\sim x^{0.79}$, indicating a narrower jet. Our predictions differ notably from most results reported in the literature. These contradictions demand revisiting jet studies involving carefully designed facilities and boundary conditions, and highly resolved simulations.

Motivated by the recent numerical results of Khalid et al. (Phys. Rev. Lett., vol. 127, 2021, 134502), we consider the large-Weissenberg-number ($W$) asymptotics of the centre mode instability in inertialess viscoelastic channel flow. The instability is of the critical layer type in the distinguished ultra-dilute limit where $W(1-\beta )=O(1)$ as $W \rightarrow \infty$ ($\beta$ is the ratio of solvent-to-total viscosity). In contrast to centre modes in the Orr–Sommerfeld equation, $1-c=O(1)$ as $W \rightarrow \infty$, where $c$ is the phase speed normalised by the centreline speed as a central ‘outer’ region is always needed to adjust the non-zero cross-stream velocity at the critical layer down to zero at the centreline. The critical layer acts as a pair of intense ‘bellows’ which blows the flow streamlines apart locally and then sucks them back together again. This compression/rarefaction amplifies the streamwise-normal polymer stress which in turn drives the streamwise flow through local polymer stresses at the critical layer. The streamwise flow energises the cross-stream flow via continuity which in turn intensifies the critical layer to close the cycle. We also treat the large-Reynolds-number ($Re$) asymptotic structure of the upper (where $1-c=O(Re^{-2/3})$) and lower branches of the $Re$–$W$ neutral curve, confirming the inferred scalings from previous numerical computations. Finally, we remark that the viscoelastic centre-mode instability was actually first observed in viscoelastic Kolmogorov flow by Boffetta et al. (J. Fluid Mech., vol. 523, 2005, pp. 161–170).

To date, a comprehensive understanding of the influence of the Prandtl number ($Pr$) on flow topology in turbulent Rayleigh–Bénard convection (RBC) remains elusive. In this study, we present an experimental investigation into the evolution of flow topology in quasi-two-dimensional turbulent RBC with $7.0 \leq Pr \leq 244.2$ and $2.03\times 10^{8} \leq Ra \leq 2.81\times 10^{9}$. Particle image velocimetry (PIV) measurements reveal the flow transitions from multiple-roll state to single-roll state with increasing $Ra$, and the transition is hindered with increasing $Pr$, i.e. the transitional Rayleigh number $Ra_t$ increases with $Pr$. We mapped out a phase diagram on the flow topology change on $Ra$ and $Pr$, and identified the scaling of $Ra_t$ on $Pr$: $Ra_t \sim Pr^{0.93}$ in the low $Pr$ range, and $Ra_t \sim Pr^{3.3}$ in the high $Pr$ range. The scaling in the low $Pr$ range is consistent with the model of balance of energy dissipation time and plume travel time that we proposed in our previous study, while the scaling in the high $Pr$ range implies a new governing mechanism. For the first time, the scaling of $Re$ on $Ra$ and $Pr$ is acquired through full-field PIV velocity measurement, $Re \sim Ra^{0.63}\,Pr^{-0.87}$. We also propose that increasing horizontal velocity promotes the formation of the large-scale circulation (LSC), especially for the high $Pr$ case. Our proposal was verified by achieving LSC through introducing horizontal driving force $Ra_H$ by tilting the convection cell with a small angle.

We employ the methods of statistical mechanics to obtain closures for the balance equations of momentum and fluctuation kinetic energy that govern the ballistic motion of grains rebounding at a rigid, bumpy bed that are driven by turbulent or non-turbulent shearing fluids, in the absence of mid-trajectory collisions and fluid velocity fluctuations. We obtain semi-analytical solutions for steady and fully developed saltation over horizontal beds for the vertical profiles of particle concentration and stresses and fluid and particle velocities. These compare favourably with measurements in discrete-element numerical simulations in the wide range of conditions of Earth and other planetary environments. The predictions of the particle horizontal mass flux and its scaling with the amount of particles in the system, the properties of the carrier fluid and the intensity of the shearing also agree with numerical simulations and wind-tunnel experiments.

The linear stability of plane Couette–Poiseuille flow (CPF) is studied with the physical effects of stratification, rotation and viscosity all included for the first time together. With no stratification, two instability mechanisms are present due to the shear and rotation which, for the most part, do not interact as they favour different forms of two-dimensionality. However, there are some small parts of parameter space where new three-dimensional instability appears indicating that Rayleigh's criterion is also violated in parameter space beyond where shear instability is expected. No fully localised centrifugal instabilities can be found for CPF, but they are shown to exist if the base flow shear has a maximum in the domain (the base flow needs to be at least cubic in the cross-stream variable rather than just quadratic as in CPF). With stable stratification present, new instabilities are found due to the combined effects of stratification and rotation, but only some appear to be of the resonance-type associated with the strato-rotational instability. The other unstable branches are more accurately interpreted as a stratification-modified centrifugal instability. Three-dimensional versions of this violate Rayleigh's criterion even when this is extended to include stratification. When stratification is stronger than rotation, the resonance-type instabilities are only dominant for cyclonic flows.

Motivated by contradicting or insufficient information regarding the large-scale flow dynamics around surface-mounted finite-height square prisms of small aspect ratio, the present study investigates the dominant vortex shedding and low-frequency dynamics around a surface-mounted cube. These flow modes were obtained from the spectral proper orthogonal decomposition of large-eddy simulation results, at a Reynolds number of $\textit {Re}=1\times 10^4$ and two different types of boundary layer: a thin and laminar boundary layer with thickness $\delta /D=0.2$ and a thick and turbulent boundary layer with $\delta /D=0.8$. The main antisymmetric mode pair revealed a new flow pattern with the alternate shedding of streamwise flow structures, indicating a transition from the half-loops of taller prisms to only streamwise strands (i.e. no vertical core) for smaller aspect ratio. The formation process of the streamwise structures is due to a reorientation of the vorticity of the arch vortex in the streamwise direction characteristic of the shed structures. The low-frequency drift mode affected the length of the recirculation region, the strength of vortex shedding, and the near-wall flow field and pressure distribution on the cube's faces, leading to low-frequency variations in the fluctuating drag and normal force coefficients. These large-scale flow dynamics were similar for both boundary layers, but minor differences were identified, related mostly to the occurrence of flow attachment and the formation of a headband vortex for the thicker boundary layer.