No CrossRef data available.
Published online by Cambridge University Press: 20 August 2024
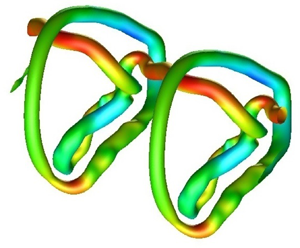
The nonlinear dynamics of a helical vortex disturbed by a long-wave-instability mode is studied by direct numerical simulation. Vortex reconnection or self-reconnection of the helical vortex is shown to play a crucial role depending on the pitch of the helical vortex. For the larger pitch, a vortex ring is created after the vortex reconnection; it detaches from the remaining helical vortex, whose pitch is doubled. A vortex ring is also created for the smaller pitch; however, it forms a linked system with the remaining vortex. The topological constraint due to this linkage forces strong interaction between the different parts of the helical vortex, leading to turbulent transition.