Published online by Cambridge University Press: 20 August 2024
We optimize jet mixing using large eddy simulations (LES) at a Reynolds number of  $3000$. Key methodological enablers consist of Bayesian optimization, a surrogate model enhanced by deep learning and persistent data topology for physical interpretation. The mixing performance is characterized by an equivalent jet radius (
$3000$. Key methodological enablers consist of Bayesian optimization, a surrogate model enhanced by deep learning and persistent data topology for physical interpretation. The mixing performance is characterized by an equivalent jet radius ( $R_{eq}$) derived from the streamwise velocity in a plane located
$R_{eq}$) derived from the streamwise velocity in a plane located  $8$ diameters downstream. The optimization is performed in a 22-dimensional actuation space that comprises most known excitations. This search space parameterizes the distributed actuation imposed on the bulk flow and at the periphery of the nozzle in the streamwise and radial directions. The momentum flux measures the energy input of the actuation. The optimization quadruples the jet radius
$8$ diameters downstream. The optimization is performed in a 22-dimensional actuation space that comprises most known excitations. This search space parameterizes the distributed actuation imposed on the bulk flow and at the periphery of the nozzle in the streamwise and radial directions. The momentum flux measures the energy input of the actuation. The optimization quadruples the jet radius  $R_{eq}$ with a
$R_{eq}$ with a  $7$-armed blooming jet after around
$7$-armed blooming jet after around  $570$ evaluations. The control input requires
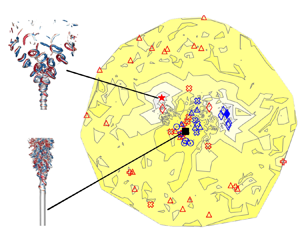
$570$ evaluations. The control input requires  $2\,\%$ momentum flux of the main flow, which is one order of magnitude lower than an ad hoc dual-mode excitation. Intriguingly, a pronounced suboptimum in the search space is associated with a double-helix jet, a new flow pattern. This jet pattern results in a mixing improvement comparable to the blooming jet. A state-of-the-art Bayesian optimization converges towards this double-helix solution. The learning is accelerated and converges to another better optimum by including a deep-learning-enhanced surrogate model trained along the optimization. Persistent data topology extracts the global and many local minima in the actuation space. These minima can be identified with flow patterns beneficial to the mixing.
$2\,\%$ momentum flux of the main flow, which is one order of magnitude lower than an ad hoc dual-mode excitation. Intriguingly, a pronounced suboptimum in the search space is associated with a double-helix jet, a new flow pattern. This jet pattern results in a mixing improvement comparable to the blooming jet. A state-of-the-art Bayesian optimization converges towards this double-helix solution. The learning is accelerated and converges to another better optimum by including a deep-learning-enhanced surrogate model trained along the optimization. Persistent data topology extracts the global and many local minima in the actuation space. These minima can be identified with flow patterns beneficial to the mixing.