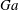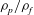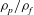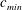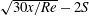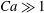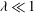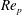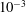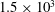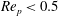Focus on Fluids
The inside view of an oscillating pipe
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
On pressure impulse of a laser-induced underwater shock wave
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 5-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
High-fidelity simulation of a standing-wave thermoacoustic–piezoelectric engine
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 19-60
-
- Article
- Export citation
Subcritical convection of liquid metals in a rotating sphere using a quasi-geostrophic model
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 61-89
-
- Article
- Export citation
Investigation of tone generation in ideally expanded supersonic planar impinging jets using large-eddy simulation
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 90-115
-
- Article
- Export citation
Compressibility effects in the shear layer over a rectangular cavity
-
- Published online by Cambridge University Press:
- 26 October 2016, pp. 116-152
-
- Article
- Export citation
Reduced particle settling speed in turbulence
-
- Published online by Cambridge University Press:
- 27 October 2016, pp. 153-167
-
- Article
- Export citation
Experimental observation of gravity–capillary solitary waves generated by a moving air suction
-
- Published online by Cambridge University Press:
- 27 October 2016, pp. 168-188
-
- Article
- Export citation
Model order reduction using sparse coding exemplified for the lid-driven cavity
-
- Published online by Cambridge University Press:
- 27 October 2016, pp. 189-223
-
- Article
- Export citation
Crossflow instability in a hypersonic boundary layer
-
- Published online by Cambridge University Press:
- 27 October 2016, pp. 224-244
-
- Article
- Export citation
Quantifying acoustic damping using flame chemiluminescence
-
- Published online by Cambridge University Press:
- 28 October 2016, pp. 245-257
-
- Article
- Export citation
Impinging planar jet flow on a horizontal surface with slip
-
- Published online by Cambridge University Press:
- 28 October 2016, pp. 258-289
-
- Article
- Export citation
Dynamic wetting failure and hydrodynamic assist in curtain coating
-
- Published online by Cambridge University Press:
- 28 October 2016, pp. 290-315
-
- Article
- Export citation
Stability of momentumless wakes
-
- Published online by Cambridge University Press:
- 28 October 2016, pp. 316-336
-
- Article
- Export citation
A slender drop in a nonlinear extensional flow
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 337-361
-
- Article
- Export citation
Axisymmetric jet manipulated using two unsteady minijets
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 362-396
-
- Article
- Export citation
Critical shear rate and torque stability condition for a particle resting on a surface in a fluid flow
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 397-409
-
- Article
- Export citation
A two-phase thermomechanical theory for granular suspensions
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 410-440
-
- Article
- Export citation
Spilling breakers in shallow water: applications to Favre waves and to the shoaling and breaking of solitary waves
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 441-468
-
- Article
- Export citation
Turbulence modifications induced by the bed mobility in intense sediment-laden flows
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 469-484
-
- Article
- Export citation