Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
van Hinsberg, M. A. T.
Clercx, H. J. H.
and
Toschi, F.
2017.
Enhanced settling of nonheavy inertial particles in homogeneous isotropic turbulence: The role of the pressure gradient and the Basset history force.
Physical Review E,
Vol. 95,
Issue. 2,
Tanaka, Mitsuru
2017.
Effect of gravity on the development of homogeneous shear turbulence laden with finite-size particles.
Journal of Turbulence,
Vol. 18,
Issue. 12,
p.
1144.
Yu, Zhaosheng
Lin, Zhaowu
Shao, Xueming
and
Wang, Lian-Ping
2017.
Effects of particle-fluid density ratio on the interactions between the turbulent channel flow and finite-size particles.
Physical Review E,
Vol. 96,
Issue. 3,
Amoura, Zouhir
Besnaci, Cédric
Risso, Frédéric
and
Roig, Véronique
2017.
Velocity fluctuations generated by the flow through a random array of spheres: a model of bubble-induced agitation.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
592.
Fornari, Walter
Ardekani, Mehdi Niazi
and
Brandt, Luca
2018.
Clustering and increased settling speed of oblate particles at finite Reynolds number.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
696.
Esfahani, Nikoo Roghani
Mobarekeh, Mohsen Nourouzi
and
Hoodaji, Mehran
2018.
Effect of Grit Chamber Configuration on Particle Removal: Using Response Surface Method.
Journal of Membrane and Separation Technology,
Vol. 7,
Issue. ,
p.
12.
Fornari, Walter
Zade, Sagar
Brandt, Luca
and
Picano, Francesco
2019.
Settling of finite-size particles in turbulence at different volume fractions.
Acta Mechanica,
Vol. 230,
Issue. 2,
p.
413.
Willen, Daniel P.
and
Prosperetti, Andrea
2019.
Resolved simulations of sedimenting suspensions of spheres.
Physical Review Fluids,
Vol. 4,
Issue. 1,
Dey, Subhasish
Zeeshan Ali, Sk
and
Padhi, Ellora
2019.
Terminal fall velocity: the legacy of Stokes from the perspective of fluvial hydraulics.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2228,
p.
20190277.
Chouippe, Agathe
and
Uhlmann, Markus
2019.
On the influence of forced homogeneous-isotropic turbulence on the settling and clustering of finite-size particles.
Acta Mechanica,
Vol. 230,
Issue. 2,
p.
387.
Tom, Josin
and
Bragg, Andrew D.
2019.
Multiscale preferential sweeping of particles settling in turbulence.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
244.
Byron, Margaret L.
Tao, Yiheng
Houghton, Isabel A.
and
Variano, Evan A.
2019.
Slip velocity of large low-aspect-ratio cylinders in homogeneous isotropic turbulence.
International Journal of Multiphase Flow,
Vol. 121,
Issue. ,
p.
103120.
Eshghinejadfard, Amir
Hosseini, Seyed Ali
and
Thévenin, Dominique
2019.
Effect of particle density in turbulent channel flows with resolved oblate spheroids.
Computers & Fluids,
Vol. 184,
Issue. ,
p.
29.
Blay Esteban, Luis
2020.
Dynamics of Non-Spherical Particles in Turbulence.
p.
121.
Zhu, Chenlin
Yu, Zhaosheng
Shao, Xueming
and
Deng, Jian
2020.
Interface-resolved numerical simulations of particle-laden turbulent flows in a vertical channel filled with Bingham fluids.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Tanaka, Mitsuru
Tajiri, Kyohei
Nishida, Hidetoshi
and
Yamakawa, Masashi
2020.
Effect of Eccentric Mass Distribution on the Motion of Spherical Particles in Shear Flows.
Journal of Fluids Engineering,
Vol. 142,
Issue. 3,
Zhu, Chenlin
Yu, Zhaosheng
Pan, Dingyi
and
Shao, Xueming
2020.
Interface-resolved direct numerical simulations of the interactions between spheroidal particles and upward vertical turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 891,
Issue. ,
Chan, Timothy T.K.
Blay Esteban, Luis
Huisman, Sander G.
Shrimpton, John S.
and
Ganapathisubramani, Bharathram
2021.
Settling behaviour of thin curved particles in quiescent fluid and turbulence.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Thurai, Merhala
Bringi, Viswanathan
Gatlin, Patrick
and
Wingo, Mathew
2021.
Raindrop fall velocity in turbulent flow: an observational study.
Advances in Science and Research,
Vol. 18,
Issue. ,
p.
33.
Yang, Bo
Peng, Cheng
Wang, Guichao
and
Wang, Lian-Ping
2021.
A direct numerical simulation study of flow modulation and turbulent sedimentation in particle-laden downward channel flows.
Physics of Fluids,
Vol. 33,
Issue. 9,
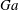 $Ga$. The Galileo number is the ratio between buoyancy and viscous forces, and is here varied via the solid-to-fluid density ratio
$Ga$. The Galileo number is the ratio between buoyancy and viscous forces, and is here varied via the solid-to-fluid density ratio 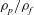 $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$. The focus is on particles that are slightly heavier than the fluid. We find that in HIT, the mean settling speed is less than that in quiescent fluid; in particular, it reduces by 6 %–60 % with respect to the terminal velocity of an isolated sphere in quiescent fluid as the ratio between the latter and the turbulent velocity fluctuations
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$. The focus is on particles that are slightly heavier than the fluid. We find that in HIT, the mean settling speed is less than that in quiescent fluid; in particular, it reduces by 6 %–60 % with respect to the terminal velocity of an isolated sphere in quiescent fluid as the ratio between the latter and the turbulent velocity fluctuations 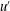 $u^{\prime }$ is decreased. Analysing the fluid–particle relative motion, we find that the mean settling speed is progressively reduced while reducing
$u^{\prime }$ is decreased. Analysing the fluid–particle relative motion, we find that the mean settling speed is progressively reduced while reducing 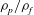 $\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$ due to the increase of the vertical drag induced by the particle cross-flow velocity. Unsteady effects contribute to the mean overall drag by about 6 %–10 %. The probability density functions of particle velocities and accelerations reveal that these are closely related to the features of the turbulent flow. The particle mean-square displacement in the settling direction is found to be similar for all
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$ due to the increase of the vertical drag induced by the particle cross-flow velocity. Unsteady effects contribute to the mean overall drag by about 6 %–10 %. The probability density functions of particle velocities and accelerations reveal that these are closely related to the features of the turbulent flow. The particle mean-square displacement in the settling direction is found to be similar for all 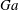 $Ga$ if time is scaled by
$Ga$ if time is scaled by 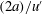 $(2a)/u^{\prime }$ (where
$(2a)/u^{\prime }$ (where 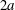 $2a$ is the particle diameter and
$2a$ is the particle diameter and 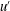 $u^{\prime }$ is the turbulence velocity root mean square).
$u^{\prime }$ is the turbulence velocity root mean square).


