Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Maffei, S.
and
Jackson, A.
2017.
Kinematic validation of a quasi-geostrophic model for the fast dynamics in the Earth’s outer core.
Geophysical Journal International,
Vol. 210,
Issue. 3,
p.
1772.
Maffei, Stefano
Jackson, Andrew
and
Livermore, Philip W.
2017.
Characterization of columnar inertial modes in rapidly rotating spheres and spheroids.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 473,
Issue. 2204,
p.
20170181.
Guervilly, C.
and
Cardin, P.
2017.
Multiple zonal jets and convective heat transport barriers in a quasi-geostrophic model of planetary cores.
Geophysical Journal International,
Vol. 211,
Issue. 1,
p.
455.
Kaplan, E. J.
Schaeffer, N.
Vidal, J.
and
Cardin, P.
2017.
Subcritical Thermal Convection of Liquid Metals in a Rapidly Rotating Sphere.
Physical Review Letters,
Vol. 119,
Issue. 9,
Tobias, S. M.
Oishi, J. S.
and
Marston, J. B.
2018.
Generalized quasilinear approximation of the interaction of convection and mean flows in a thermal annulus.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 474,
Issue. 2219,
Bardsley, O. P.
2018.
Could hydrodynamic Rossby waves explain the westward drift?.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 474,
Issue. 2213,
p.
20180119.
Aurnou, Jonathan M.
Bertin, Vincent
Grannan, Alexander M.
Horn, Susanne
and
Vogt, Tobias
2018.
Rotating thermal convection in liquid gallium: multi-modal flow, absent steady columns.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
846.
More, Colin
and
Dumberry, Mathieu
2018.
Convectively driven decadal zonal accelerations in Earth’s fluid core.
Geophysical Journal International,
Vol. 213,
Issue. 1,
p.
434.
Lam, Kameng
Kong, Dali
and
Zhang, Keke
2018.
Nonlinear thermal inertial waves in rotating fluid spheres.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 112,
Issue. 5,
p.
357.
Kong, Dali
Zhang, Keke
Lam, Kameng
and
Willis, Ashley P.
2018.
Axially symmetric and latitudinally propagating nonlinear patterns in rotating spherical convection.
Physical Review E,
Vol. 98,
Issue. 3,
Guervilly, Céline
Cardin, Philippe
and
Schaeffer, Nathanaël
2019.
Turbulent convective length scale in planetary cores.
Nature,
Vol. 570,
Issue. 7761,
p.
368.
Sánchez Umbría, J.
and
Net, M.
2019.
Torsional solutions of convection in rotating fluid spheres.
Physical Review Fluids,
Vol. 4,
Issue. 1,
Gastine, Thomas
2019.
pizza: an open-source pseudo-spectral code for spherical quasi-geostrophic convection.
Geophysical Journal International,
Vol. 217,
Issue. 3,
p.
1558.
Moffatt, Keith
and
Dormy, Emmanuel
2019.
Self-Exciting Fluid Dynamos.
Monville, R
Vidal, J
Cébron, D
and
Schaeffer, N
2019.
Rotating double-diffusive convection in stably stratified planetary cores.
Geophysical Journal International,
Vol. 219,
Issue. Supplement_1,
p.
S195.
Menaut, Rémi
Corre, Yoann
Huguet, Ludovic
Le Reun, Thomas
Alboussière, Thierry
Bergman, Michael
Deguen, Renaud
Labrosse, Stéphane
and
Moulin, Marc
2019.
Experimental study of convection in the compressible regime.
Physical Review Fluids,
Vol. 4,
Issue. 3,
Aurnou, Jonathan M.
Horn, Susanne
and
Julien, Keith
2020.
Connections between nonrotating, slowly rotating, and rapidly rotating turbulent convection transport scalings.
Physical Review Research,
Vol. 2,
Issue. 4,
Kumar, Abhishek
and
Pothérat, Alban
2020.
Mixed baroclinic convection in a cavity.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Jackson, Andrew
and
Maffei, Stefano
2020.
Plesio-geostrophy for Earth’s core: I. Basic equations, inertial modes and induction.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 476,
Issue. 2243,
Lin, Yufeng
and
Jackson, Andrew
2021.
Large-scale vortices and zonal flows in spherical rotating convection.
Journal of Fluid Mechanics,
Vol. 912,
Issue. ,
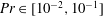 $Pr\in [10^{-2},10^{-1}]$). We use a numerical model based on the quasi-geostrophic approximation, in which variations of the axial vorticity along the rotation axis are neglected, whereas the temperature field is fully three-dimensional. We identify two separate branches of convection close to onset: (i) a well-known weak branch for Ekman numbers greater than
$Pr\in [10^{-2},10^{-1}]$). We use a numerical model based on the quasi-geostrophic approximation, in which variations of the axial vorticity along the rotation axis are neglected, whereas the temperature field is fully three-dimensional. We identify two separate branches of convection close to onset: (i) a well-known weak branch for Ekman numbers greater than 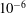 $10^{-6}$, which is continuous at the onset (supercritical bifurcation) and consists of thermal Rossby waves and (ii) a novel strong branch at lower Ekman numbers, which is discontinuous at the onset. The strong branch becomes subcritical for Ekman numbers of the order of
$10^{-6}$, which is continuous at the onset (supercritical bifurcation) and consists of thermal Rossby waves and (ii) a novel strong branch at lower Ekman numbers, which is discontinuous at the onset. The strong branch becomes subcritical for Ekman numbers of the order of 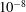 $10^{-8}$. On the strong branch, the Reynolds number of the flow is greater than
$10^{-8}$. On the strong branch, the Reynolds number of the flow is greater than 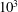 $10^{3}$, and a strong zonal flow with multiple jets develops, even close to the nonlinear onset of convection. We find that the subcriticality is amplified by decreasing the Prandtl number. The two branches can co-exist for intermediate Ekman numbers, leading to hysteresis (
$10^{3}$, and a strong zonal flow with multiple jets develops, even close to the nonlinear onset of convection. We find that the subcriticality is amplified by decreasing the Prandtl number. The two branches can co-exist for intermediate Ekman numbers, leading to hysteresis (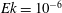 $Ek=10^{-6}$,
$Ek=10^{-6}$, 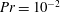 $Pr=10^{-2}$). Nonlinear oscillations are observed near the onset of convection for
$Pr=10^{-2}$). Nonlinear oscillations are observed near the onset of convection for  $Ek=10^{-7}$ and
$Ek=10^{-7}$ and  $Pr=10^{-1}$.
$Pr=10^{-1}$.


