The interactions of two like-signed vortices in viscous fluid are investigated using two-dimensional numerical simulations performed across a range of vortex strength ratios, 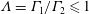 $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6E4}_{1}/\unicode[STIX]{x1D6E4}_{2}\leqslant 1$, corresponding to vortices of circulation,
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6E4}_{1}/\unicode[STIX]{x1D6E4}_{2}\leqslant 1$, corresponding to vortices of circulation, 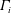 $\unicode[STIX]{x1D6E4}_{i}$, with differing initial size and/or peak vorticity. In all cases, the vortices evolve by viscous diffusion before undergoing a primary convective interaction, which ultimately results in a single vortex. The post-interaction vortex is quantitatively evaluated in terms of an enhancement factor,
$\unicode[STIX]{x1D6E4}_{i}$, with differing initial size and/or peak vorticity. In all cases, the vortices evolve by viscous diffusion before undergoing a primary convective interaction, which ultimately results in a single vortex. The post-interaction vortex is quantitatively evaluated in terms of an enhancement factor, 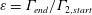 $\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6E4}_{end}/\unicode[STIX]{x1D6E4}_{2,start}$, which compares its circulation,
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6E4}_{end}/\unicode[STIX]{x1D6E4}_{2,start}$, which compares its circulation, 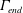 $\unicode[STIX]{x1D6E4}_{end}$, to that of the stronger starting vortex,
$\unicode[STIX]{x1D6E4}_{end}$, to that of the stronger starting vortex, 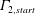 $\unicode[STIX]{x1D6E4}_{2,start}$. Results are effectively characterized by a mutuality parameter,
$\unicode[STIX]{x1D6E4}_{2,start}$. Results are effectively characterized by a mutuality parameter, 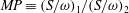 $MP\equiv (S/\unicode[STIX]{x1D714})_{1}/(S/\unicode[STIX]{x1D714})_{2}$, where the ratio of induced strain rate,
$MP\equiv (S/\unicode[STIX]{x1D714})_{1}/(S/\unicode[STIX]{x1D714})_{2}$, where the ratio of induced strain rate, 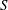 $S$, to peak vorticity,
$S$, to peak vorticity, 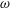 $\unicode[STIX]{x1D714}$, for each vortex,
$\unicode[STIX]{x1D714}$, for each vortex, 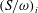 $(S/\unicode[STIX]{x1D714})_{i}$, is found to have a critical value,
$(S/\unicode[STIX]{x1D714})_{i}$, is found to have a critical value, 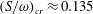 $(S/\unicode[STIX]{x1D714})_{cr}\approx 0.135$, above which core detrainment occurs. If
$(S/\unicode[STIX]{x1D714})_{cr}\approx 0.135$, above which core detrainment occurs. If 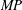 $MP$ is sufficiently close to unity, both vortices detrain and a two-way mutual entrainment process leads to
$MP$ is sufficiently close to unity, both vortices detrain and a two-way mutual entrainment process leads to 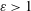 $\unicode[STIX]{x1D700}>1$, i.e. merger. In asymmetric interactions and mergers, generally one vortex dominates; the weak/no/strong vortex winner regimes correspond to
$\unicode[STIX]{x1D700}>1$, i.e. merger. In asymmetric interactions and mergers, generally one vortex dominates; the weak/no/strong vortex winner regimes correspond to 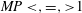 $MP<,=,>1$, respectively. As
$MP<,=,>1$, respectively. As 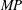 $MP$ deviates from unity,
$MP$ deviates from unity,  $\unicode[STIX]{x1D700}$ decreases until a critical value,
$\unicode[STIX]{x1D700}$ decreases until a critical value, 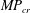 $MP_{cr}$ is reached, beyond which there is only a one-way interaction; one vortex detrains and is destroyed by the other, which dominates and survives. There is no entrainment and
$MP_{cr}$ is reached, beyond which there is only a one-way interaction; one vortex detrains and is destroyed by the other, which dominates and survives. There is no entrainment and 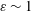 $\unicode[STIX]{x1D700}\sim 1$, i.e. only a straining out occurs. Although
$\unicode[STIX]{x1D700}\sim 1$, i.e. only a straining out occurs. Although 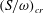 $(S/\unicode[STIX]{x1D714})_{cr}$ appears to be independent of Reynolds number,
$(S/\unicode[STIX]{x1D714})_{cr}$ appears to be independent of Reynolds number, 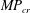 $MP_{cr}$ shows a dependence. Comparisons are made with available experimental data from Meunier (2001, PhD thesis, Université de Provence-Aix-Marseille I).
$MP_{cr}$ shows a dependence. Comparisons are made with available experimental data from Meunier (2001, PhD thesis, Université de Provence-Aix-Marseille I).