Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T17:13:53.852Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of three-dimensional columnar convection in a porous medium

Published online by Cambridge University Press:  14 September 2017

Duncan R. Hewitt Open the ORCID record for Duncan R. Hewitt [Opens in a new window]  and
John R. Lister
Duncan R. Hewitt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
John R. Lister
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of steady convective exchange flow with a rectangular planform in an unbounded three-dimensional porous medium is explored. The base flow comprises a balance between vertical advection with amplitude 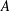$A$ in interleaving rectangular columns with aspect ratio 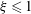$\unicode[STIX]{x1D709}\leqslant 1$ and horizontal diffusion between the columns. Columnar flow with a square planform (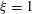$\unicode[STIX]{x1D709}=1$) is found to be weakly unstable to a large-scale perturbation of the background temperature gradient, irrespective of 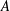$A$, but to have no stronger instability on the scale of the columns. This result provides a stark contrast to two-dimensional columnar flow (Hewitt et al., J. Fluid Mech., vol. 737, 2013, pp. 205–231), which, as 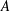$A$ is increased, is increasingly unstable to a perturbation on the scale of the columnar wavelength. For rectangular planforms with 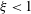$\unicode[STIX]{x1D709}<1$, a critical aspect ratio is identified, below which a perturbation on the scale of the columns is the fastest growing mode, as in two dimensions. Scalings for the growth rate and the structure of this mode are identified, and are explained by means of an asymptotic expansion in the limit 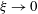$\unicode[STIX]{x1D709}\rightarrow 0$. The difference between the stabilities of two-dimensional and three-dimensional exchange flow provides a potential explanation for the apparent difference in dominant horizontal scale observed in direct numerical simulations of two-dimensional and three-dimensional statistically steady ‘Rayleigh–Darcy’ convection at high Rayleigh numbers.

JFM classification

Convection: Convection in porous media Instability: Instability Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 89 - 111
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Stability of columnar convection in a porous medium. J. Fluid Mech. 737, 205–231.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.Google Scholar
Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16, 367–370.CrossRefGoogle Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.Google Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Math. Proc. Camb. Phil. Soc. 44, 508–521.Google Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media, 3rd edn. Springer.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.CrossRefGoogle Scholar
Phillips, O. M. 2009 Geological Fluid Dynamics: Sub-surface Flow and Reactions. Cambridge University Press.Google Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377, 2931–2938.Google Scholar
Wen, B., Corson, L. T. & Chini, G. P. 2015 Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid Mech. 772, 197–224.Google Scholar