Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-09T22:09:10.821Z Has data issue: false hasContentIssue false
  • English
  • Français

The ‘hanging flag’ problem: on the heaving motion of a thin filament in the limit of small flexural stiffness

Published online by Cambridge University Press:  14 September 2017

A. Manela Open the ORCID record for A. Manela [Opens in a new window]  and
M. Weidenfeld
A. Manela*
Affiliation:
Faculty of Aerospace Engineering, Technion – Israel Institute of Technology, Technion City, Haifa 32000, Israel
M. Weidenfeld
Affiliation:
Faculty of Aerospace Engineering, Technion – Israel Institute of Technology, Technion City, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the fluid–structure interaction of a vertically hanging filament immersed in uniform incompressible high Reynolds number flow. The filament is subject to small-amplitude harmonic heaving at its upstream edge, and to a gravity-induced (‘hanging chain’) tension force. We focus on the limit of small bending rigidity to examine the differences between a highly elastic beam (where bending rigidity is small but finite) and a membrane (where bending rigidity vanishes). The problem is analysed by means of thin airfoil theory, in conjunction with a discrete vortex model for the downstream wake. Denoting the filament non-dimensional rigidity (normalized by the tension force) by 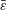$\bar{\unicode[STIX]{x1D700}}$, it is first verified that the beam deflection and associated flow field converge to the membrane solution at 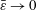$\bar{\unicode[STIX]{x1D700}}\rightarrow 0$. At low actuation frequencies, the differences between the membrane and beam motions are small, and both follow a nearly rigid-body motion parallel to the upstream-edge actuation. With increasing frequency, the differences between the beam and membrane become visible at increasingly lower values of 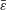$\bar{\unicode[STIX]{x1D700}}$, and the stabilizing effect of beam flexural rigidity, resulting in reduced flapping amplitudes, is apparent. Examining the beam motion near its edge points at non-small frequencies, semi-analytic approximations for the associated time-periodic displacements are obtained. Close to the actuated end, a layer of width 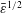$\bar{\unicode[STIX]{x1D700}}^{1/2}$ is found, where the flexural rigidity term in the equation of motion is balanced by the tension term. Here, the differences between the beam and membrane deflections are attributed to the additional zero-slope condition satisfied by the former. In the vicinity of the free end, a local Taylor expansion is carried out. A balance between the bending and inertia terms results in a layer of width 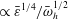$\propto \bar{\unicode[STIX]{x1D700}}^{1/4}/\bar{\unicode[STIX]{x1D714}}_{h}^{1/2}$, where 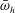$\bar{\unicode[STIX]{x1D714}}_{h}$ denotes the scaled heaving frequency. The layer is therefore thicker than the upstream layer for 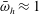$\bar{\unicode[STIX]{x1D714}}_{h}\approx 1$, and becomes thinner with increasing 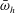$\bar{\unicode[STIX]{x1D714}}_{h}$. Within the layer, the beam deflects linearly with the distance from the edge, in marked difference from a membrane and in accordance with the free-end conditions satisfied by the former.

JFM classification

Aerodynamics: Aerodynamics Aerodynamics: Flow-structure interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 190 - 213
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. 2008 Optimal flexibility of a flapping appendage in an inviscid fluid. J. Fluid Mech. 614, 355–380.Google Scholar
Alben, S. & Shelley, M. J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100, 074301.Google Scholar
Allen, J. J. & Smits, A. J. 2001 Energy harvesting eel. J. Fluids Struct. 15, 629–640.CrossRefGoogle Scholar
Antman, S. S. 2004 Nonlinear Problems of Elasticity. Springer.Google Scholar
Bailey, H. 2000 Motion of a hanging chain after the free end is given an initial velocity. Am. J. Phys. 68, 764–767.CrossRefGoogle Scholar
Belmonte, A., Shelley, M. J., Eldakar, S. T. & Wiggins, C. H. 2001 Dynamic patterns and self-knotting of a driven hanging chain. Phys. Rev. Lett. 87, 114301.Google Scholar
Datta, S. K. & Gottenberg, W. G. 1975 Instability of an elastic strip hanging in an airstream. J. Appl. Mech. 42, 195–198.Google Scholar
Denoel, V. & Canor, T. 2013 Patching asymptotics solution of a cable with a small bending stiffness. J. Struct. Engng 139, 180–187.Google Scholar
Dowell, E. H. & Ventres, C. S. 1970 Flutter of low aspect ratio plates. AIAA J. 8, 1162–1164.CrossRefGoogle Scholar
Gibbs, S. C. & Dowell, E. H. 2014 Membrane paradox for solar sails. AIAA J. 52, 2904–2906.Google Scholar
Hagedorn, P. & Dasgupta, A. 2007 Vibrations and Waves in Continuous Mechanical Systems. Wiley.CrossRefGoogle Scholar
Howe, M. S. 1996 Emendation of the Brown & Michael equation, with application to sound generation by vortex motion near a half-plane. J. Fluid Mech. 329, 89–101.Google Scholar
Huang, L. 1995 Mechanical modeling of palatal snoring. J. Acoust. Soc. Am. 97, 3642–3648.Google Scholar
Huang, W.-X. & Sung, H. J. 2010 Three-dimensional simulation of a flapping flag in a uniform flow. J. Fluid Mech. 653, 301–336.CrossRefGoogle Scholar
Kevorkian, J. & Cole, J. D. 1981 Perturbation Methods in Applied Mathematics. Springer.Google Scholar
Lakin, W. D. 1975 Eigenvalues of a slightly stiff pendulum with a small bob. J. Engng Maths 9, 207–218.CrossRefGoogle Scholar
Lemaitre, C., Hemon, P. & de Langre, E. 2005 Instability of a long ribbon hanging in axial air flow. J. Fluids Struct. 20, 913–925.CrossRefGoogle Scholar
Liao, J. C., Beal, D. N., Lauder, G. V. & Triantafyllou, M. S. 2003 Fish exploiting vortices decrease muscle activity. Science 302, 1566–1569.Google Scholar
Manela, A. 2012 Vibration and sound of an elastic wing actuated at its leading edge. J. Sound Vib. 331, 638–650.Google Scholar
Manela, A. & Howe, M. S. 2009 The forced motion of a flag. J. Fluid Mech. 635, 439–454.Google Scholar
Manela, A. & Huang, L. 2013 Point vortex model for prediction of sound generated by a wing with flap interacting with a passing vortex. J. Acoust. Soc. Am. 133, 1934–1944.Google Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 Resonance and propulsion performance of a heaving flexible wing. Phys. Fluids 21, 071902.Google Scholar
Peters, M. C. A. M. & Hirschberg, A. 1993 Acoustically induced periodic vortex shedding at sharp edged open channel ends: simple vortex models. J. Sound Vib. 161, 281–299.Google Scholar
Saffman, P. & Baker, G. 1979 Vortex interactions. Annu. Rev. Fluid Mech. 11, 95–122.Google Scholar
Sarpkaya, T. 1989 Computational methods with vortices – the 1988 freeman scholar lecure. J. Fluids Engng 11, 5–52.Google Scholar
Sarradj, E., Fritzsche, C. & Geyer, T. 2011 Silent owl flight: bird flyover noise measurements. AIAA J. 49, 769–779.CrossRefGoogle Scholar
Schafer, B. 1985 Free vibrations of a gravity-loaded clamped-free beam. Ing.-Arch. 55, 66–80.CrossRefGoogle Scholar
Shelley, M. J. & Zhang, J. 2011 Flapping and bending bodies interacting with fluid flows. Annu. Rev. Fluid Mech. 43, 449–465.Google Scholar
Spriggs, J. H., Messiter, A. F. & Anderson, W. J. 1969 Membrane flutter paradox – an explanation by singular-perturbation methods. AIAA J. 7, 1704–1709.CrossRefGoogle Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. No. 496.Google Scholar