Article contents
Control of viscous instability by variation of injection rate in a fluid with time-dependent rheology
Published online by Cambridge University Press: 14 September 2017
Abstract
Using variational calculus, we investigate the time-dependent injection rate that minimises the growth of the Saffman–Taylor instability when a finite volume of fluid is injected in a finite time, 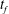 $t_{f}$, into a Hele-Shaw cell. We first consider a planar interface, and show that, with a constant viscosity ratio, the constant injection rate is optimal. When the viscosity of the displacing fluid,
$t_{f}$, into a Hele-Shaw cell. We first consider a planar interface, and show that, with a constant viscosity ratio, the constant injection rate is optimal. When the viscosity of the displacing fluid, 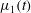 $\unicode[STIX]{x1D707}_{1}(t)$, gradually increases over time, as may occur with a slowly gelling polymer solution, the optimal injection rate,
$\unicode[STIX]{x1D707}_{1}(t)$, gradually increases over time, as may occur with a slowly gelling polymer solution, the optimal injection rate, 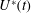 $U^{\ast }(t)$, involves a gradual increase in the flow rate with time. This leads to a smaller initial value of flow rate than the constant injection rate, finishing with a larger value. Such optimisation can lead to a substantial suppression of the instability as compared to the constant injection case if the characteristic gelling time is comparable to
$U^{\ast }(t)$, involves a gradual increase in the flow rate with time. This leads to a smaller initial value of flow rate than the constant injection rate, finishing with a larger value. Such optimisation can lead to a substantial suppression of the instability as compared to the constant injection case if the characteristic gelling time is comparable to 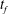 $t_{f}$. In contrast, for either relatively slow or fast gelling, there is much less benefit in selecting the optimal injection rate,
$t_{f}$. In contrast, for either relatively slow or fast gelling, there is much less benefit in selecting the optimal injection rate, 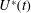 $U^{\ast }(t)$, as compared to the constant injection rate. In the case of a constant injection rate from a point source,
$U^{\ast }(t)$, as compared to the constant injection rate. In the case of a constant injection rate from a point source, 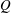 $Q$, then with a constant viscosity ratio the fastest-growing perturbation on the radially spreading front involves axisymmetric modes whose wavenumber increases with time. Approximating the discrete azimuthal modes by a continuous distribution, we find the injection rate that minimises growth,
$Q$, then with a constant viscosity ratio the fastest-growing perturbation on the radially spreading front involves axisymmetric modes whose wavenumber increases with time. Approximating the discrete azimuthal modes by a continuous distribution, we find the injection rate that minimises growth, 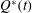 $Q^{\ast }(t)$. We find that there is a critical time for injection,
$Q^{\ast }(t)$. We find that there is a critical time for injection, 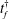 $t_{f}^{\dagger }$, such that if
$t_{f}^{\dagger }$, such that if 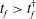 $t_{f}>t_{f}^{\dagger }$ then
$t_{f}>t_{f}^{\dagger }$ then  $Q^{\ast }(t)$ can be chosen so that the interface is always stable. This critical time emerges from the case with an injection rate given by
$Q^{\ast }(t)$ can be chosen so that the interface is always stable. This critical time emerges from the case with an injection rate given by 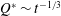 $Q^{\ast }\sim t^{-1/3}$. As the total injection time is reduced to values
$Q^{\ast }\sim t^{-1/3}$. As the total injection time is reduced to values 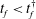 $t_{f}<t_{f}^{\dagger }$, the system becomes progressively more unstable, and the optimal injection rate for an idealised continuous distribution of azimuthal modes asymptotes to a flow rate that increases linearly with time. As for the one-dimensional case, if the viscosity of the injection fluid gradually increases over time, then the optimal injection rate has a smaller initial value but gradually increases to larger values than for the analogous constant viscosity problem. If the displacing fluid features shear-thinning rheology, then the optimal injection rate involves a smaller flow rate at early times, although not as large a reduction as in the Newtonian case, and a larger flow rate at late times, although not as large an increase as in the Newtonian case.
$t_{f}<t_{f}^{\dagger }$, the system becomes progressively more unstable, and the optimal injection rate for an idealised continuous distribution of azimuthal modes asymptotes to a flow rate that increases linearly with time. As for the one-dimensional case, if the viscosity of the injection fluid gradually increases over time, then the optimal injection rate has a smaller initial value but gradually increases to larger values than for the analogous constant viscosity problem. If the displacing fluid features shear-thinning rheology, then the optimal injection rate involves a smaller flow rate at early times, although not as large a reduction as in the Newtonian case, and a larger flow rate at late times, although not as large an increase as in the Newtonian case.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 10
- Cited by



