Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-24T22:42:39.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Experiments on, and discrete and continuum simulations of, the discharge of granular media from silos with a lateral orifice

Published online by Cambridge University Press:  21 September 2017

Y. Zhou ,
P.-Y. Lagrée ,
S. Popinet ,
P. Ruyer  and
P. Aussillous Open the ORCID record for P. Aussillous [Opens in a new window]
Y. Zhou
Affiliation:
Institut de Radioprotection et de Sûreté Nucléaire (IRSN), PSN-RES, SEMIA, LIMAR, Cadarache, St Paul-Lez-Durance, 13115, France Aix-Marseille Univ, CNRS, IUSTI, Marseille, France
P.-Y. Lagrée
Affiliation:
Sorbonne Universités, UPMC Univ Paris 06, CNRS UMR 7190, Institut Jean le Rond $\unicode[STIX]{x2202}^{\prime }$Alembert, F-75005 Paris, France
S. Popinet
Affiliation:
Sorbonne Universités, UPMC Univ Paris 06, CNRS UMR 7190, Institut Jean le Rond $\unicode[STIX]{x2202}^{\prime }$Alembert, F-75005 Paris, France
P. Ruyer
Affiliation:
Institut de Radioprotection et de Sûreté Nucléaire (IRSN), PSN-RES, SEMIA, LIMAR, Cadarache, St Paul-Lez-Durance, 13115, France
P. Aussillous*
Affiliation:
Aix-Marseille Univ, CNRS, IUSTI, Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

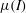We compare laboratory experiments, contact dynamics simulations and continuum Navier–Stokes simulations with a $\unicode[STIX]{x1D707}(I)$ visco-plastic rheology, of the discharge of granular media from a silo with a lateral orifice. We consider a rectangular silo with an orifice of height 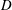$D$ which spans the silo width 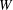$W$, and we observe two regimes. For small enough aperture aspect ratio 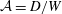${\mathcal{A}}=D/W$, the Hagen–Beverloo relation is obtained. For thin enough silos, 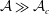${\mathcal{A}}\gg {\mathcal{A}}_{c}$, we observe a second regime where the outlet velocity varies with 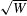$\sqrt{W}$. This new regime is also obtained in the continuum simulations when the friction on side walls is taken into account in a thickness-averaged version of $\unicode[STIX]{x1D707}(I)$ 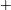$+$ Navier–Stokes (in the spirit of Hele-Shaw flows). Moreover most of the internal details of the flow field observed experimentally are reproduced when considering this lateral friction. These two regimes are recovered experimentally for a cylindrical silo with a lateral rectangular orifice of height 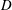$D$ and arc length 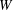$W$. The dependency of the flow rate on the particle diameter is found to be reasonably described experimentally using two geometrical functions that depend respectively on the number of beads through the two aperture dimensions. This is consistent with two-dimensional discrete simulation results: at the outlet, the volume fraction and the velocities depend on the particle diameter and this behaviour is correctly described by those geometrical functions. A similar dependency is observed in the two-dimensional continuum simulations.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 459 - 485
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aguirre, M. A., Grande, J. G., Calvo, A., Pugnaloni, L. A. & Géminard, J.-C. 2010 Pressure independence of granular flow through an aperture. Phys. Rev. Lett. 104, 238002.CrossRefGoogle ScholarPubMed
Benyamine, M., Djermane, M., Dalloz-Dubrujeaud, B. & Aussillous, P. 2014 Discharge flow of a bidisperse granular media from a silo. Phys. Rev. E 90, 032201.Google ScholarPubMed
Bertho, Y., Giorgiutti-Dauphiné, F. & Hulin, J.-P. 2003 Dynamical Janssen effect on granular packing with moving walls. Phys. Rev. Lett. 90 (14), 144301.Google Scholar
Beverloo, W. A., Leniger, H. A. & Van de Velde, J. 1961 The flow of granular solids through orifices. Chem. Engng Sci. 15, 260–269.Google Scholar
Choi, J., Kudrolli, A. & Bazant, M. Z. 2005 Velocity profile of granular flows inside silos and hoppers. J. Phys.: Condens. Matter 17, S2533–S2548.Google Scholar
Davier, G. & Bertails-Descoubes, F. 2016 Nonsmooth simulation of dense granular flows with pressure-dependent yield stress. J. Non-Newtonian Fluid 234, 15–35.Google Scholar
Dunatunga, S. & Kamrin, K. 2015 Continuum modelling and simulation of granular flows through their many phases. J. Fluid Mech. 779, 483–513.Google Scholar
Janda, A., Zuriguel, I. & Maza, D. 2012 Flow rate of particles through apertures obtained from self-similar density and velocity profiles. Phys. Rev. Lett. 108, 248001.CrossRefGoogle ScholarPubMed
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441, 727–730.Google Scholar
Lagrée, P.-Y. 2007 Interactive boundary layer in a Hele Shaw cell. Z. Angew. Math. Mech. 87 (7), 489–498.Google Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a Navier–Stokes model with a 𝜇(I)-rheology. J. Fluid Mech. 686, 378–408.Google Scholar
Medina, A., Cabrera, D., López-Villa, A. & Pliego, M. 2014 Discharge rates of dry granular material from bins with lateral exit holes. Powder Technol. 253, 270–275.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and treatment of errors due to high velocity gradients in particle image velocimetry. Exp. Fluids 35 (5), 408–421.CrossRefGoogle Scholar
Midi, G. D. R. 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Perge, C., Aguirre, M. A., Gago, P. A., Pugnaloni, L. A., Tourneau, D. L. & Géminard, J. C. 2012 Evolution of pressure profiles during the discharge of a silo. Phys. Rev. E 85, 021303.CrossRefGoogle ScholarPubMed
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.Google Scholar
Popinet, S.2013–2016 Basilisk C reference manual. http://basilisk.fr/Basilisk%20C.Google Scholar
Radjai, F. & Dubois, F. 2011 Discrete-Element Modeling of Granular Materials. Wiley.Google Scholar
Rubio-Largo, S. M., Janda, A., Maza, D., Zuriguel, I. & Hidalgo, R. C. 2015 Disentangling the free-fall arch paradox in silo discharge. Phys. Rev. Lett. 114, 238002.Google Scholar
Serrano, D. A., Medina, A., Chavarria, G. R., Pliego, M. & Klapp, J. 2015 Mass flow rate of granular material flowing from tilted bins. Powder Technol. 286, 438–443.Google Scholar
Sheldon, H. G. & Durian, D. J. 2010 Granular discharge and clogging for tilted hoppers. Granul. Matt. 12, 579–585.Google Scholar
Staron, L., Lagrée, P.-Y. & Popinet, S. 2012 The granular silo as a continuum plastic flow: The hour-glass versus the clepsydra. Phys. Fluids 24, 103301.Google Scholar
Staron, L., Lagrée, P.-Y. & Popinet, S. 2014 Continuum simulation of the discharge of the granular silo, a validation test for the 𝜇(I) visco-plastic flow law. Eur. Phys. J. E 37 (1), 5.Google Scholar
Tighe, B. P. & Sperl, M. 2007 Pressure and motion of dry sand: translation of Hagen’s paper from 1852. Granul. Matt. 9, 141–144.Google Scholar
Zhou, Y., Ruyer, P. & Aussillous, P. 2015 Discharge flow of a bidisperse granular media from a silo: discrete particle simulations. Phys. Rev. E 92, 062204.Google Scholar
Supplementary material: File

Zhou et al. supplementary material

Zhou et al. supplementary material 1

Download Zhou et al. supplementary material(File)
File 3.3 KB