Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T11:49:59.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation

Published online by Cambridge University Press:  20 September 2017

V. Kitsios Open the ORCID record for V. Kitsios [Opens in a new window] ,
A. Sekimoto Open the ORCID record for A. Sekimoto [Opens in a new window] ,
C. Atkinson ,
J. A. Sillero ,
G. Borrell ,
A. G. Gungor ,
J. Jiménez Open the ORCID record for J. Jiménez [Opens in a new window]  and
J. Soria Open the ORCID record for J. Soria [Opens in a new window]
V. Kitsios*
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia CSIRO Oceans and Atmosphere, Hobart 3700, Australia
A. Sekimoto
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
C. Atkinson
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia
J. A. Sillero
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, E-28040 Madrid, Spain
G. Borrell
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, E-28040 Madrid, Spain
A. G. Gungor
Affiliation:
Department of Astronautical Engineering, Istanbul Technical University, Maslak 34469 Istanbul, Turkey
J. Jiménez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Pza. Cardenal Cisneros 3, E-28040 Madrid, Spain
J. Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton 3800, Australia Department of Aeronautical Engineering, King Abdulaziz University, Jeddah 21589, Kingdom of Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The statistical properties are presented for the direct numerical simulation of a self-similar adverse pressure gradient (APG) turbulent boundary layer (TBL) at the verge of separation. The APG TBL has a momentum thickness-based Reynolds number range from 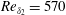$Re_{\unicode[STIX]{x1D6FF}_{2}}=570$ to 13 800, with a self-similar region from 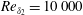$Re_{\unicode[STIX]{x1D6FF}_{2}}=10\,000$ to 12 300. Within this domain the average non-dimensional pressure gradient parameter 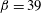$\unicode[STIX]{x1D6FD}=39$, where for a unit density 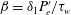$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FF}_{1}P_{\!e}^{\prime }/\unicode[STIX]{x1D70F}_{w}$, with 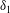$\unicode[STIX]{x1D6FF}_{1}$ the displacement thickness, 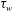$\unicode[STIX]{x1D70F}_{w}$ the mean shear stress at the wall and 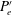$P_{\!e}^{\prime }$ the far-field pressure gradient. This flow is compared with previous zero pressure gradient and mild APG TBL (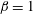$\unicode[STIX]{x1D6FD}=1$) results of similar Reynolds number. All flows are generated via the direct numerical simulation of a TBL on a flat surface with far-field boundary conditions tailored to apply the desired pressure gradient. The conditions for self-similarity, and the appropriate length and velocity scales, are derived. The mean and Reynolds stress profiles are shown to collapse when non-dimensionalised on the basis of these length and velocity scales. As the pressure gradient increases, the extent of the wake region in the mean streamwise velocity profiles increases, whilst the extent of the log-layer and viscous sublayer decreases. The Reynolds stress, production and dissipation profiles of the APG TBL cases exhibit a second outer peak, which becomes more pronounced and more spatially localised with increasing pressure gradient. This outer peak is located at the point of inflection of the mean velocity profiles, and is suggestive of the presence of a shear flow instability. The maximum streamwise velocity variance is located at a wall normal position of 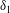$\unicode[STIX]{x1D6FF}_{1}$ of spanwise wavelength of 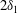$2\unicode[STIX]{x1D6FF}_{1}$. In summary as the pressure gradient increases the flow has properties less like a zero pressure gradient TBL and more akin to a free shear layer.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 392 - 419
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
Araya, G. & Castillo, L. 2013 Direct numerical simulations of turbulent thermal boundary layers subjected to adverse streamwise pressure gradients. Phys. Fluids 25, 095107.CrossRefGoogle Scholar
Atkinson, C., Buchner, A.-J., Sekimoto, A., Kitsios, V. & Soria, J. 2016 Experimental measurements of a self-similar adverse pressure gradient turbulent boundary layer. In Proceedings of the 20th Australasian Fluid Mechanics Conference, Perth, Australia, Australasian Fluid Mechanics Society.Google Scholar
Aubertine, C. D. & Eaton, J. K. 2005 Turbulence development in a non-equilibrium turbulent boundary layer with mild adverse pressure gradient. J. Fluid Mech. 532, 345–364.Google Scholar
Borrell, G., Sillero, J. A. & Jiménez, J. 2013 A code for direct numerical simulation of turbulent boundary layers at high Reynolds numbers in BG/P supercomputers. Comput. Fluids 80, 37–43.Google Scholar
Castillo, L. & Wang, X. 2004 Similarity analysis for nonequilibrium turbulent boundary layers. Trans. ASME J. Fluids Engng 126, 827–834.CrossRefGoogle Scholar
Chawla, T. C. & Tennekes, H. 1973 Turbulent boundary layers with negligible wall stress: a singular-perturbation theory. Intl J. Engng Sci. 11, 45–64.Google Scholar
Cheng, W., Pullin, D. I. & Samtaney, R. 2015 Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer. J. Fluid Mech. 785, 78–108.CrossRefGoogle Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.CrossRefGoogle Scholar
Cutler, A. D. & Johnston, J. P. 1989 The relaxation of a turbulent boundary layer in an adverse pressure gradient. J. Fluid Mech. 200, 367–387.CrossRefGoogle Scholar
Durbin, P. A. & Belcher, S. E. 1992 Scaling of adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 238, 699–722.Google Scholar
Elsberry, K., Loeffler, F., Zhou, M. D. & Wygnanski, I. 2000 An experimental study of a boundary layer that is maintained on the verge of separation. J. Fluid Mech. 423, 227–261.CrossRefGoogle Scholar
George, W. K. & Castillo, L. 1993 Boundary layers with pressure gradient: another look at the equilibrium boundary layer. In Near Wall Turbulence. Elsevier.Google Scholar
Gungor, A. G., Maciel, Y., Simens, M. P. & Soria, J. 2016 Scaling and statistics of large-defect adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 59, 109–124.CrossRefGoogle Scholar
Gungor, A. G., Simens, M. P. & Jiménez, J. 2012 Direct numerical simulation of wake-perturbed separated boundary layers. J. Turbul. 134, 061024.Google Scholar
Harlow, F. H. & Welch, J. E. 1965 Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 8 (12), 2182–2189.Google Scholar
Kitsios, V., Atkinson, C., Sillero, J., Borrell, G., Gungor, A. G., Jiménez, J. & Soria, J. 2016 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer. Intl J. Heat Fluid Flow 61 (A), 129–136.Google Scholar
Kitsios, V., Cordier, L., Bonnet, J.-P., Ooi, A. & Soria, J. 2010 Development of a non-linear eddy viscosity closure for the triple decomposition stability analysis of a turbulent channel. J. Fluid Mech. 664, 74–107.Google Scholar
Kitsios, V., Cordier, L., Bonnet, J.-P., Ooi, A. & Soria, J. 2011 On the coherent structures and stability properties of a leading edge separated airfoil with turbulent recirculation. J. Fluid Mech. 683, 395–416.Google Scholar
Lee, J.-H. & Sung, J. 2008 Effects of an adverse pressure gradient on a turbulent boundary layer. Intl J. Heat Fluid Flow 29, 568–578.CrossRefGoogle Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
Lighthill, M. J. 1963 Introduction. Boundary layer theory. In Laminar Boundary Layers. Oxford University Press.Google Scholar
Maciel, Y., Rossignol, K.-S. & Lemay, J. 2006 Self-similarity in the outer region of adverse-pressure-gradient. AIAA J. 44, 2450–2464.Google Scholar
Marusic, I. & Perry, A. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Mathis, R., Duke, D., Kitsios, V. & Soria, J. 2008 Use of zero-net-mass-flow for separation control in diffusing s-duct. Exp. Therm. Fluid Sci. 33, 169–172.CrossRefGoogle Scholar
Mellor, G. L. 1966 The effects of pressure gradients on turbulent flow near a smooth wall. J. Fluid Mech. 24, 255–274.Google Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24, 225–253.Google Scholar
Monty, J., Harun, Z. & Marusic, I. 2011 A parametric study of adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 32, 575–585.Google Scholar
Na, Y. & Moin, P. 1998 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.Google Scholar
Nickels, T. B. 2004 Inner scaling for wall-bounded flows subject to large pressure gradients. J. Fluid Mech. 521, 217–239.CrossRefGoogle Scholar
Perot, J. B. 1993 An analysis of the fractional step method. J. Comput. Phys. 108, 51–58.Google Scholar
Perry, A. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hpothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Perry, A., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rahgozar, S. & Maciel, Y. 2011 Low- and high-speed structures in the outer region of an adverse pressure gradient turbulent boundary layer. Exp. Therm. Fluid Sci. 35, 1575–1587.Google Scholar
Rheinboldt, W. 1956 Zur außeren randbedingung bei den grenzschichtgleichungen. Z. Angew. Math. Mech. 36, 153–154.Google Scholar
Sillero, J.2014 High Reynolds number turbulent boundary layers. PhD thesis, Universidad Politénica de Madrid.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25, 105102.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26, 105109.Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4128–4231.Google Scholar
Simpson, R. L., Strickland, J. H. & Barr, P. W. 1977 Features of a separating turbulent boundary layer in the vicinity of separation. J. Fluid Mech. 79, 553–594.CrossRefGoogle Scholar
Skåre, P. E. & Krogstad, P.-A. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.CrossRefGoogle Scholar
Skote, M. & Henningson, D. S. 2002 Direct numerical simulaiton of a separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.Google Scholar
Skote, M., Henningson, D. & Henkes, R. A. W. M. 1998 Direct numerical simulation of self-similar turbulent boundary layers in adverse pressure gradients. Flow Turbul. Combust. 60, 47–85.CrossRefGoogle Scholar
Spalart, P. & Watmuff, J. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.CrossRefGoogle Scholar
Stratford, B. S. 1959 An experimental flow with zero skin friction throughout its region of pressure rise. J. Fluid Mech. 8, 143–155.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A. A. 1960 The development of turbulent boundary layers with negligible wall stress. J. Fluid Mech. 8, 143–155.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar