The presence of a no-slip, impermeable, adiabatic, sloped boundary in an otherwise quiescent, stably stratified, Boussinesq flow generates baroclinic vorticity within a diffusive boundary layer. Such conditions are typical of the oscillating boundary layers on adiabatic abyssal slopes, sloped lake bathymetry and sloped coastal bathymetry in the absence of high-wavenumber internal waves, mean flows, far-field turbulence on larger scales, and resonant tidal–bathymetric interaction. We investigate the linear stability of the oscillating flow within non-dimensional parameter space typical of the 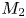 $M_2$ tide and hydraulically smooth, middle-latitude abyssal slopes through Floquet linear stability analysis. The flow dynamics depends on three non-dimensional variables: the Reynolds number for Stokes’ second problem, the Prandtl number, and a frequency ratio that accounts for the resonance conditions (
$M_2$ tide and hydraulically smooth, middle-latitude abyssal slopes through Floquet linear stability analysis. The flow dynamics depends on three non-dimensional variables: the Reynolds number for Stokes’ second problem, the Prandtl number, and a frequency ratio that accounts for the resonance conditions ( $C$, criticality) of the buoyant restoring force and the tidal forcing. The Floquet analysis results suggest that oscillating laminar boundary layers on adiabatic abyssal slopes are increasingly unstable as Reynolds number, criticality parameter and/or spanwise disturbance wavenumber are increased. We also show that the two-dimensional Floquet linear instability necessarily generates three-dimensional baroclinic vorticity, which suggests that the evolution of the gravitational instabilities may be nonlinear as
$C$, criticality) of the buoyant restoring force and the tidal forcing. The Floquet analysis results suggest that oscillating laminar boundary layers on adiabatic abyssal slopes are increasingly unstable as Reynolds number, criticality parameter and/or spanwise disturbance wavenumber are increased. We also show that the two-dimensional Floquet linear instability necessarily generates three-dimensional baroclinic vorticity, which suggests that the evolution of the gravitational instabilities may be nonlinear as 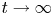 $t\rightarrow \infty$.
$t\rightarrow \infty$.