The present study investigates the profiles of statistically axisymmetric turbulent jets with arbitrary buoyancy. Analytical expressions for the shape of the radial velocity, Reynolds stress and radial scalar flux profiles are derived from the governing equations by assuming self-similar Gaussian mean velocity and scalar profiles. Previously these have only been derived for the special cases of pure jets and plumes, whereas the present study generalises them to arbitrary buoyancies. These are then used to derive analytical expressions for the turbulent Schmidt/Prandtl numbers, which, along with the mean profiles, are shown to give predictions in agreement with existing literature.

Direct numerical simulations were performed to characterize fully developed supersonic turbulent channel flows over isothermal rough walls. The effect of roughness was incorporated using a level-set/volume-of-fluid immersed boundary method. Turbulence statistics of five channel flows are compared, including one reference case with both walls smooth and four cases with smooth top walls and bottom walls with two-dimensional (2-D) and three-dimensional (3-D) sinusoidal roughnesses. Results reveal a strong dependence of the turbulence on the roughness topography and the associated shock patterns. Specifically, the 2-D geometries generate strong oblique shock waves that propagate across the channel and are reflected back to the rough-wall side. These strong shocks are absent in the smooth-wall channel and are significantly weaker in cases with 3-D roughness geometries, replaced by weak shocklets. At the impingement locations of the shocks on the top wall in the 2-D roughness cases, localized augmentations of turbulence shear production are observed. Such regions of augmented production also exist for the 3-D cases, at a much weaker level. The oblique shock waves are thought to be responsible for a more significant entropy generation for cases with 2-D surfaces than those with 3-D ones, leading to a higher irreversible heat generation and consequently higher temperature values in 2-D roughness cases. In the present supersonic channels, the effects of roughness extend beyond the near-wall layer due to the shocks. This suggests that outer layer similarity may not fully apply to a rough-wall supersonic turbulent flow.

We present the analytical solution for the two-dimensional velocity and density fields within an approximation for laminar stratified inclined duct (SID) flows where diffusion dominates over inertia in the along-channel momentum equation but is negligible in the density transport equation. We refer to this approximation as the hydrostatic/gravitational/viscous in momentum and advective in density (HGV-A) approximation due to the leading balances in the governing equations. The analytical solution is valid for laminar flows in a two-layer configuration in the limit of long ducts. The non-dimensional volume flux within the HGV-A approximation is given by $Fr^* ={{Re}}_g/(AK)$, which is a control parameter with ${{Re}}_g$ the gravitational Reynolds number, $A$ the aspect ratio of the duct and $K$ a geometrical parameter that depends on the tilt of the duct and is obtained from the analytical solution. This analytical solution was validated against results from laboratory experiments, and allows us to gain new insight into the dynamics and properties of SID flows. Most importantly, constant values of $Fr^*$ describe, in both horizontal and inclined ducts, the transitions between increasingly turbulent flow regimes: from laminar flow, to interfacial waves, to intermittent turbulence and sustained turbulence.

Mixing of fluids in a coaxial jet is studied under four distinct viscosity ratios, $m=1$, $10$, $20$ and $40$, using highly resolved large-eddy simulations (LES), particle image velocimetry and planar laser-induced fluorescence. The accuracy of predictions is tested against data obtained by the simultaneous experimental measurements of velocity and concentration fields. For the highest and lowest viscosity ratios, standard RANS models with unclosed terms pertaining to viscosity variations are employed. We show that the standard Reynolds-averaged Navier–Stokes (RANS) approach with no explicit modelling for variable-viscosity terms is not applicable whereas dynamic LES models provide high-quality agreement with the measurements. To identify the underlying mixing physics and sources of discrepancy in RANS predictions, two distinct mixing modes are defined based on the viscosity ratio. Then, for each mode, the evolution of mixing structures, momentum budget analysis with emphasis on variable-viscosity terms, analysis of the turbulent activity and decay of turbulence are investigated using highly resolved LES data. The mixing dynamics is found to be quite distinct in each mixing mode. Variable viscosity manifests multiple effects that are working against each other. Viscosity gradients induce additional instabilities while increasing overall viscosity decreases the effective Reynolds number leading to laminarization of the turbulent jet, explaining the lack of dispersion and turbulent diffusion. Momentum budget analysis reveals that variable-viscosity terms are significant to be neglected. The scaling of the energy spectrum cascade suggests that in the TLL mode the unsteady laminar shedding is responsible for the eddies observed.

We derive a scaling law for the characteristic frequencies of wall pressure fluctuations in swept shock wave/turbulent boundary layer interactions in the presence of cylindrical symmetry, based on analysis of a direct numerical simulations database. Direct numerical simulations in large domains show evidence of spanwise rippling of the separation line, with typical wavelength proportional to separation bubble size. Pressure disturbances around the separation line are shown to be convected at a phase speed proportional to the cross-flow velocity. This information is leveraged to derive a simple model for low-frequency unsteadiness, which extends previous two-dimensional models (Piponniau et al., J. Fluid Mech., vol. 629, 2009, pp. 87–108), and which correctly predicts growth of the typical frequency with the sweep angle. Inferences regarding the typical frequencies in more general swept shock wave/turbulent boundary layer interactions are also discussed.

We consider the stability of laminar high-Reynolds-number flow through a planar channel formed by a rigid wall and a heavy compliant wall under longitudinal tension with motion resisted by structural damping. Numerical simulations indicate that the baseline state (with Poiseuille flow and a flat wall) exhibits two unstable normal modes: the Tollmien–Schlichting (TS) mode and a surface-based mode which manifests as one of two flow-induced surface instabilities (FISI), known as travelling wave flutter (TWF) and static divergence (SD), respectively. In the absence of wall damping the system is unstable to TWF, where the neutrally stable wavelength becomes shorter as the wall mass increases. With wall damping, TWF is restricted to long wavelengths through interaction with the most unstable centre mode, while for wall damping greater than a critical value the system exhibits an SD mode with a two branch neutral stability curve; the critical conditions along the upper and lower branches are constructed in the limit of large wall damping. We compute the Reynolds–Orr and activation energy descriptions of these neutrally stable FISI by continuing the linear stability analysis to the following order in perturbation amplitude. We find that both FISI are primarily driven by the working of normal stress on the flexible wall, lower-branch SD has negative activation energy, while upper-branch SD approaches zero activation energy in the limit of large wall damping. Finally, we elucidate interaction between TS and TWF modes for large wall mass, resulting in stable islands within unstable regions of parameter space.

We study the effect of insoluble surfactants on the spatio-temporal evolution of turbulent jets. We use three-dimensional numerical simulations and employ an interface-tracking/level-set method that accounts for surfactant-induced Marangoni stresses. The present study builds on our previous work (Constante-Amores et al., J. Fluid Mech., vol. 922, 2021, A6) in which we examined in detail the vortex–surface interaction in the absence of surfactants. Numerical solutions are obtained for a wide range of Weber and elasticity numbers in which vorticity production is generated by surface deformation and surfactant-induced Marangoni stresses. The present work demonstrates, for the first time, the crucial role of Marangoni stresses, brought about by surfactant concentration gradients, in the formation of coherent, hairpin-like vortex structures. These structures have a profound influence on the development of the three-dimensional interfacial dynamics. We also present theoretical expressions for the mechanisms that influence the rate of production of circulation in the presence of surfactants for a general, three-dimensional, two-phase flow, and highlight the dominant contribution of surfactant-induced Marangoni stresses.

When a cylinder is mounted on an elastic support within a current, vortex-induced vibrations (VIV) may occur down to a Reynolds number (Re) close to 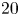$20$, based on the body diameter (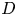$D$) and inflow velocity ($U$), i.e. below the critical value of 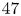$47$ reported for the onset of flow unsteadiness when the body is fixed. The impact of a forced rotation of the elastically mounted cylinder on the system behaviour is explored numerically for 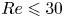$Re \leqslant 30$, over wide ranges of values of the rotation rate (ratio between body surface velocity and 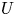$U$, 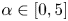$\alpha \in [0,5]$) and reduced velocity (inverse of the oscillator natural frequency non-dimensionalized by $D$ and $U$, 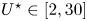$U^\star \in [2,30]$). The influence of the rotation is not monotonic, but the most prominent effect uncovered in this work is a substantial enhancement of the subcritical-Re, flow-induced vibrations beyond $\alpha =2$. This enhancement is twofold. First, the rotation results in a considerable expansion of the vibration/flow unsteadiness region in the 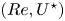$({Re},U^\star )$ domain, down to 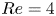$Re=4$. Second, the elliptical orbits described by the rotating body are subjected to a major amplification, with a transition from VIV to responses whose magnitude tends to increase unboundedly with 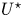$U^\star$, even though still synchronized with flow unsteadiness. The emergence of such galloping-like oscillations close to the onset of vibrations disrupts the scenario of gradual vibration growth with Re, as amplitudes larger than 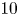$10$ body diameters may be observed at $Re=10$.

Recent works on wall-bounded flows have corroborated the coexistence of wall-attached eddies, whose statistical features are predicted through Townsend's attached-eddy hypothesis (AEH), and very-large-scale motions (VLSMs). Furthermore, it has been shown that the presence of wall-attached eddies within the logarithmic layer is linked to the appearance of an inverse-power-law region in the streamwise velocity energy spectra, upon significant separation between outer and viscous scales. In this work, a near-neutral atmospheric surface layer is probed with wind light detection and ranging to investigate the contributions to the streamwise velocity energy associated with wall-attached eddies and VLSMs for a very-high-Reynolds-number boundary layer. Energy and linear coherence spectra (LCS) of the streamwise velocity are interrogated to identify the spectral boundaries associated with eddies of different typologies. Inspired by the AEH, an analytical model for the LCS associated with wall-attached eddies is formulated. The experimental results show that the identification of the wall-attached-eddy energy contribution through the analysis of the energy spectra leads to an underestimate of the associated spectral range, maximum height attained and turbulence intensity. This feature is due to the overlap of the energy associated with VLSMs obscuring the inverse-power-law region. The LCS analysis estimates wall-attached eddies with a streamwise/wall-normal ratio of about 14.3 attaining a height of about 30 % of the outer scale of turbulence.

Reliable prediction of the erosion rate of sediment beds is important for many applications in coastal and river engineering. Theoretical understanding of empirically derived scaling relations is still lacking. This applies in particular for the scaling anomaly between low and high Shields number conditions. In this work, the erosion process is studied from the perspective of the phase-averaged turbulent kinetic energy (TKE) equations. The multi-phase TKE equations are written in a form that allows for a direct comparison with the TKE equation that appears for a stratified single-phase flow under the Boussinesq approximation. This reveals that next to buoyancy destruction, several other TKE modulation mechanisms become important at high Shields numbers and concentrations. Two scaling laws are derived for both moderate and high Shields numbers, and are tested against a wide range of experimental data.

Geophysical mass flows such as debris flows, dense pyroclastic flows and snow avalanches can self-channelize on shallow slopes. The confinement afforded by formed levees helps to maintain the flow depth, and hence mobility, allowing self-channelized flows to run out significantly farther than unconfined, spreading flows. Levee formation and self-channelization are strongly associated with particle-size segregation, but can also occur in monodisperse flows. This paper uses the monodisperse depth-averaged theory of Rocha et al. (J. Fluid Mech., vol. 876, 2019, pp. 591–641), which incorporates a hysteretic friction law and second-order depth-averaged viscous terms. Both of these are vital for the formation of a travelling wave that progressively deposits a pair of levees just behind the front. The three-dimensional velocity field is reconstructed in a frame moving with the front assuming Bagnold flow. This enables a bidisperse particle-size segregation theory to be used to solve for the large and small particle concentrations and particle paths in three-dimensions, for the first time. The model shows that the large particles tend to segregate to the surface of the flow, forming a carapace that extends over the centre of the channel, as well as along the external sides and base of the levee walls. The small particles segregate downwards, and are concentrated in the main channel and in the inner levee walls. This supports the contention that a low-friction channel lining provides a secondary mechanism for run-out enhancement. It is also shown that the entire theory scales with particle diameter, so experiments with millimetre-sized particles provide important insights into geophysical-scale flows with boulders and smaller rock fragments. The model shows that self-channelization does not need particle-size segregation to occur, but supports the hypothesis that particle-size segregation and the associated frictional feedback can significantly enhance both the flow mobility and the levee strength.

The fluid–structure interactions between flexible fibres and viscous flows play an essential role in various biological phenomena, medical problems and industrial processes. Of particular interest is the case of particles transported freely in time-dependent flows. This work elucidates the dynamics and morphologies of actin filaments under oscillatory shear flows by combining microfluidic experiments, numerical simulations and theoretical modelling. Our work reveals that, in contrast to steady shear flows, in which small orientational fluctuations from a flow-aligned state initiate tumbling and deformations, the periodic flow reversal allows the filament to explore many different configurations at the beginning of each cycle. Investigation of filament motion during half time periods of oscillation highlights the critical role of the initial filament orientation on the emergent dynamics. This strong coupling between orientation and deformation results in new deformation regimes and novel higher-order buckling modes absent in steady shear flows. The primary outcome of our analysis is the possibility of suppression of buckling instabilities for certain combinations of the oscillation frequency and initial filament orientation, even in very strong flows. We explain this unusual behaviour through a weakly nonlinear Landau theory of buckling, in which we treat the filaments as inextensible Brownian Euler–Bernoulli rods whose hydrodynamics is described by local slender-body theory.

We propose a novel nonlinear manifold learning from snapshot data and demonstrate its superiority over proper orthogonal decomposition (POD) for shedding-dominated shear flows. Key enablers are isometric feature mapping, Isomap, as encoder and, $K$-nearest neighbours ($K$NN) algorithm as decoder. The proposed technique is applied to numerical and experimental datasets including the fluidic pinball, a swirling jet and the wake behind a couple of tandem cylinders. Analysing the fluidic pinball, the manifold is able to describe the pitchfork bifurcation and the chaotic regime with only three feature coordinates. These coordinates are linked to the vortex-shedding phases and the force coefficients. The manifold coordinates of the swirling jet are comparable to the POD mode amplitudes, yet allow for a more distinct and less noise-sensitive manifold identification. A similar observation is made for the wake of two tandem cylinders. The tandem cylinders are aligned and located at a streamwise distance which corresponds to the transition between the single bluff body and the reattachment regimes of vortex shedding. Isomap unveils these two shedding regimes while the Lissajous plot of the first two POD mode amplitudes features a single circle. The reconstruction error of the manifold model is small compared with the fluctuation level, indicating that the low embedding dimensions contain the coherent structure dynamics. The proposed Isomap–$K$NN manifold learner is expected to be of great importance in estimation, dynamic modelling and control for a large range of configurations with dominant coherent structures.

The Rayleigh–Taylor instability at the interface of two sheared fluid layers in a horizontal channel is investigated in the absence of inertia. The dynamics of the flow is described by a nonlinear lubrication equation which is solved numerically for adverse density stratifications. The early-time dynamics features a number of finger-like protrusions of different heights at the interface. The fingers travel at different speeds leading to a sequence of merging events after which the interface eventually settles to a near-saturated state, comprising only one finger that includes most of the lower fluid. For sufficiently large density stratifications, the final state spans the height of the channel and includes two thin fluid films at each wall, both of which undergo chaotic dynamics, but finite-time touch-down/touch-up is shown to be precluded by the shear flow. An asymptotic analysis in the large-Bond-number limit (intense density stratification) reveals the finer structure of the final state including Landau–Levich-type connection regions. The asymptotic solutions are compared with numerical results of the lubrication model as well as direct numerical simulations, and excellent agreement is observed between the three in terms of interfacial structure, wave speed and film thicknesses.

The prediction of trajectories of buoyancy-driven objects immersed in a viscous fluid is a key problem in fluid dynamics. Simple-shaped objects, such as disks, present a great variety of trajectories, ranging from zig-zag to tumbling and chaotic motions. Yet, similar studies are lacking when the object is permeable. We perform a linear stability analysis of the steady vertical path of a thin permeable disk, whose flow through the microstructure is modelled via a stress-jump model based on homogenization theory. The relative velocity of the flow associated with the vertical steady path presents a recirculation region detached from the body, which shrinks and eventually disappears as the disk becomes more permeable. In analogy with the solid disk, one non-oscillatory and several oscillatory modes are identified and found to destabilize the fluid–solid coupled system away from its straight trajectory. Permeability progressively filters out the wake dynamics in the instability of the steady vertical path. Modes dominated by wake oscillations are first stabilized, followed by those characterized by weaker, or absent, wake oscillations, in which the wake is typically a tilting induced by the disk inclined trajectory. For sufficiently large permeabilities, the disk first undergoes a non-oscillatory divergence instability, which is expected to lead to a steady oblique path with a constant disk inclination, in the nonlinear regime. A further permeability increase reduces the unstable range of all modes until quenching of all linear instabilities.

The hydrodynamics of turbulent oscillatory flow over a gravel-based irregular rough wall is investigated using laser-Doppler anemometry measurements of velocities in a large oscillatory flow tunnel and direct numerical simulation (DNS) of the Navier–Stokes equations. The same periodic irregular roughness was used for both experiments and DNS. Four flow shapes are investigated: sinusoidal, skewed, asymmetric and combined skewed–asymmetric. The experiments were conducted for target Reynolds numbers (based on the Stokes length and standard deviation of free-stream velocity) of $R_{\delta,\sigma }=800$ and $R_{\delta,\sigma }=1549$; DNS was conducted for flows with target $R_{\delta,\sigma }=800$. Boundary layer thickness, bottom phase lead and friction factor are in good agreement with previous studies. For the first time, evidence of Prandtl's secondary flows of the second kind in oscillatory flow is presented. Turbulence structure is visualised using isosurfaces of $\lambda _{2}$ (Jeong & Hussain J. Fluid Mech., vol. 285, 1995, pp. 69–94), revealing densely packed structures that grow stronger and weaker in correspondence with the free-stream velocity. Reynolds and dispersive stresses peak just below the highest roughness crest, with dispersive stress vanishing a short distance above the roughness. Bursts of turbulence kinetic energy and wake kinetic energy are generated each flow half-cycle, with variable behaviour depending on flow shape. Non-Gaussian turbulence statistics are observed that originate near the wall, becoming increasingly non-Gaussian far from the wall. Probability density functions of turbulence statistics can be closely approximated by a fourth-order Gram–Charlier distribution at most phases and elevations, though when statistics deviate more strongly from Gaussian, streamwise and wall-normal (spanwise) statistics are better described by a Pearson type IV (VII) distribution.

We consider suspensions of finite-size neutrally buoyant rigid spherical particles in channel flow and investigate the relevance of different momentum transfer mechanisms and the relation between the local particle dynamics and the bulk flow properties in the highly inertial regime. Interface-resolved simulations are performed in the range of Reynolds numbers $3000 \leq Re \leq 15\ 000$ and solid volume fractions $0 \leq \phi \leq 0.3$. The Lagrangian particle statistics show that pair interactions are highly inhomogeneous and dependent on the distance from the wall: in their vicinity, the underlying mean shear drives the pair interactions, while a high degree of isotropy, dictated by more frequent collisions, characterizes the core region. Analysis of the momentum balance reveals that while the particle-induced stresses govern the dynamics in dense conditions, $\phi =0.3$, and moderate Reynolds numbers, $Re <10\ 000$, the turbulent stresses take over at higher Reynolds numbers. This behaviour is associated with a reduced particle migration toward the channel core, which decreases the importance of the particle-induced stress and increases the turbulent activity. Our results indicate that Reynolds stresses and the associated velocity fluctuations, characteristics of near-wall turbulence, prevail at high inertia over the resistance to deformation presented by the particles for volume fractions lower than 30 %.

Dynamic mode decomposition (DMD) describes complex dynamic processes through a hierarchy of simpler coherent features. DMD is regularly used to understand the fundamental characteristics of turbulence and is closely related to Koopman operators. However, verifying the decomposition, equivalently the computed spectral features of Koopman operators, remains a significant challenge due to the infinite-dimensional nature of Koopman operators. Challenges include spurious (unphysical) modes and dealing with continuous spectra, which both occur regularly in turbulent flows. Residual dynamic mode decomposition (ResDMD), introduced by Colbrook & Townsend (Rigorous data-driven computation of spectral properties of Koopman operators for dynamical systems. 2021. arXiv:2111.14889), overcomes such challenges through the data-driven computation of residuals associated with the full infinite-dimensional Koopman operator. ResDMD computes spectra and pseudospectra of general Koopman operators with error control and computes smoothed approximations of spectral measures (including continuous spectra) with explicit high-order convergence theorems. ResDMD thus provides robust and verified Koopmanism. We implement ResDMD and demonstrate its application in various fluid dynamic situations at varying Reynolds numbers from both numerical and experimental data. Examples include vortex shedding behind a cylinder, hot-wire data acquired in a turbulent boundary layer, particle image velocimetry data focusing on a wall-jet flow and laser-induced plasma acoustic pressure signals. We present some advantages of ResDMD: the ability to resolve nonlinear and transient modes verifiably; the verification of learnt dictionaries; the verification of Koopman mode decompositions; and spectral calculations with reduced broadening effects. We also discuss how a new ordering of modes via residuals enables greater accuracy than the traditional modulus ordering (e.g. when forecasting) with a smaller dictionary. This result paves the way for more significant dynamic compression of large datasets without sacrificing accuracy.