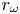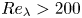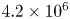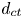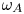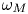Open access
JFM Papers
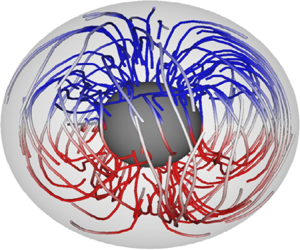
Turbulence and heat transfer on a rotating, heated half soap bubble
-
- Published online by Cambridge University Press:
- 11 August 2021, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Image-based blood flow estimation using a semi-analytical solution to the advection–diffusion equation in cylindrical domains
-
- Published online by Cambridge University Press:
- 11 August 2021, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds-number scaling of a vorticity-annihilating boundary layer
-
- Published online by Cambridge University Press:
- 06 August 2021, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Perspectives
Stability and the transition to turbulence in the flow through conduits with compliant walls
-
- Published online by Cambridge University Press:
- 05 August 2021, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Local vortex line topology and geometry in turbulence
-
- Published online by Cambridge University Press:
- 05 August 2021, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The relation between wave asymmetry and particle orbits analysed by Slepian models
-
- Published online by Cambridge University Press:
- 05 August 2021, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition from shear-dominated to Rayleigh–Taylor turbulence
-
- Published online by Cambridge University Press:
- 05 August 2021, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear dynamics of fully developed swirling jets
-
- Published online by Cambridge University Press:
- 05 August 2021, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correlation-based flow decomposition and statistical analysis of the eddy forcing
-
- Published online by Cambridge University Press:
- 04 August 2021, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
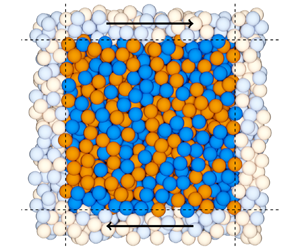
Drag, diffusion and segregation in inertial granular flows
-
- Published online by Cambridge University Press:
- 04 August 2021, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Rapids
Microtomographic particle image velocimetry measurements of viscoelastic instabilities in a three-dimensional microcontraction
-
- Published online by Cambridge University Press:
- 02 August 2021, R6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
On water waves generated by a bottom obstacle translating at a subcritical speed
-
- Published online by Cambridge University Press:
- 02 August 2021, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Leading-edge bluntness effects on hypersonic three-dimensional flows over a compression ramp
-
- Published online by Cambridge University Press:
- 30 July 2021, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Marangoni instability triggered by selective evaporation of a binary liquid inside a Hele-Shaw cell
-
- Published online by Cambridge University Press:
- 27 July 2021, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vortex dynamics on a Möbius strip
-
- Published online by Cambridge University Press:
- 22 July 2021, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scattering of entropy waves into sound by isolated aerofoils
-
- Published online by Cambridge University Press:
- 22 July 2021, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
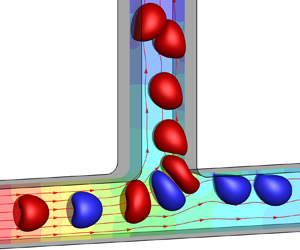
Path selection of a train of spherical capsules in a branched microchannel
-
- Published online by Cambridge University Press:
- 22 July 2021, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
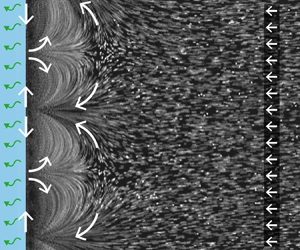
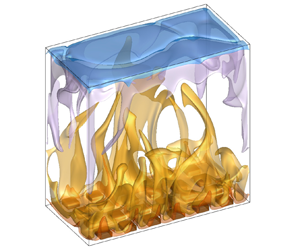
On the role of roughness valleys in turbulent Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 21 July 2021, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A wide-spacing approximation model for the reflection and transmission of water waves over an array of vertical obstacles
-
- Published online by Cambridge University Press:
- 21 July 2021, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
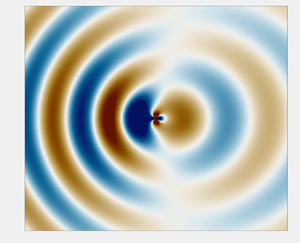
Evolution of forced magnetohydrodynamic waves in a stratified fluid
-
- Published online by Cambridge University Press:
- 19 July 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation