We prove the Gross–Deligne conjecture on CM periods for motives associated with ${{H}^{2}}$ of certain surfaces fibered over the projective line. Then we prove for the same motives a formula which expresses the ${{K}_{1}}$-regulators in terms of hypergeometric functions $_{3}{{F}_{2}}$, and obtain a new example of non-trivial regulators.

We study ${{\text{w}}^{*}}$-semicrossed products over actions of the free semigroup and the free abelian semigroup on (possibly non-selfadjoint) ${{\text{w}}^{*}}$-closed algebras. We show that they are reflexive when the dynamics are implemented by uniformly bounded families of invertible row operators. Combining with results of Helmer, we derive that ${{\text{w}}^{*}}$-semicrossed products of factors (on a separableHilbert space) are reflexive. Furthermore, we show that ${{\text{w}}^{*}}$-semicrossed products of automorphic actions on maximal abelian self adjoint algebras are reflexive. In all cases we prove that the ${{\text{w}}^{*}}$-semicrossed products have the bicommutant property if and only if the ambient algebra of the dynamics does also.

In this paper, we investigate Dirichlet spaces ${{D}_{\mu }}$ with superharmonic weights induced by positive Borel measures $\mu $ on the open unit disk. We establish the Alexander-Taylor-Ullman inequality for ${{D}_{\mu }}$ spaces and we characterize the cases where equality occurs. We define a class of weighted Hardy spaces $H_{\mu }^{2}$ via the balayage of the measure $\mu $ . We show that ${{D}_{\mu }}$ is equal to $H_{\mu }^{2}$ if and only if $\mu $ is a Carleson measure for ${{D}_{\mu }}$ . As an application, we obtain the reproducing kernel of ${{D}_{\mu }}$ when $\mu $ is an infinite sum of point-mass measures. We consider the boundary behavior and innerouter factorization of functions in ${{D}_{\mu }}$. We also characterize the boundedness and compactness of composition operators on ${{D}_{\mu }}$.

For any family of $N\,\times \,N$ random matrices ${{\left( {{\text{A}}_{k}} \right)}_{k\in K}}$ that is invariant, in law, under unitary conjugation, we give general sufficient conditions for central limit theorems for random variables of the type $\text{Tr}\left( {{\text{A}}_{k}}\text{M} \right)$, where the matrix $\text{M}$ is deterministic (such random variables include, for example, the normalized matrix entries of ${{\text{A}}_{k}}$). A consequence is the asymptotic independence of the projection of the matrices ${{\text{A}}_{k}}$ onto the subspace of null trace matrices from their projections onto the orthogonal of this subspace. These results are used to study the asymptotic behavior of the outliers of a spiked elliptic random matrix. More precisely, we show that the fluctuations of these outliers around their limits can have various rates of convergence, depending on the Jordan Canonical Form of the additive perturbation. Also, some correlations can arise between outliers at a macroscopic distance from each other.These phenomena have already been observed with random matrices from the Single Ring Theorem.

For a division ring $D$, denote by ${{\mathcal{M}}_{D}}$ the $D$-ring obtained as the completion of the direct limit $\underset{\to n}{\mathop \lim }\,{{M}_{{{2}^{n}}}}(D)$ with respect to themetric induced by its unique rank function. We prove that, for any ultramatricial $D$-ring $B$ and any non-discrete extremal pseudo-rank function $N$ on $B$, there is an isomorphism of $D$-rings $\overline{B}\,\cong \,{{\mathcal{M}}_{D}}$, where $\overline{B}$ stands for the completion of $B$ with respect to the pseudo-metric induced by $N$. This generalizes a result of von Neumann. We also show a corresponding uniqueness result for $*$-algebras over fields $\text{F}$ with positive definite involution, where the algebra ${{\mathcal{M}}_{\text{F}}}$ is endowed with its natural involution coming from the $*$-transpose involution on each of the factors ${{M}_{{{2}^{n}}}}\,(F)$.

Let ${{\Theta }^{[j]}}$ be an analogue of the Ramanujan theta operator for Siegel modular forms. For a given prime $p$ , we give the weights of elements of mod $p$ kernel of ${{\Theta }^{[j]}}$ , where the mod $p$ kernel of ${{\Theta }^{[j]}}$ is the set of all Siegel modular forms $F$ such that ${{\Theta }^{[j]}}(F)$ is congruent to zero modulo $p$ . In order to construct examples of the mod $p$ kernel of ${{\Theta }^{[j]}}$ from any Siegel modular forms, we introduce new operators ${{A}^{(j)}}(M)$ and show the modularity of $F|{{A}^{\left( j \right)}}\left( M \right)$ when $F$ is a Siegel modular form. Finally, we give some examples of the mod $p$ kernel of ${{\Theta }^{[j]}}$ and the filtrations of some of them.

We study comparison properties in the category $\text{Cu}$ aiming to lift results to the ${{\text{C}}^{\text{*}}}$-algebraic setting. We introduce a new comparison property and relate it to both the corona factorization property $\left( \text{CFP} \right)$ and $\omega $-comparison. We show differences of all properties by providing examples that suggest that the corona factorization for ${{\text{C}}^{\text{*}}}$-algebras might allow for both finite and infinite projections. In addition, we show that Rørdam's simple, nuclear ${{\text{C}}^{\text{*}}}$-algebra with a finite and an inifnite projection does not have the $\text{CFP}$.

Given a link $L$, the Blanchfield pairing $\text{Bl(}L\text{)}$ is a pairing that is defined on the torsion submodule of the Alexander module of $L$. In some particular cases, namely if $L$ is a boundary link or if the Alexander module of $L$ is torsion, $\text{Bl(}L\text{)}$ can be computed explicitly; however no formula is known in general. In this article, we compute the Blanchfield pairing of any link, generalizing the aforementioned results. As a corollary, we obtain a new proof that the Blanchfield pairing is Hermitian. Finally, we also obtain short proofs of several properties of $\text{Bl(}L\text{)}$.

We study restriction and extension properties for states on ${{\text{C}}^{*}}$-algebras with an eye towards hyperrigidity of operator systems. We use these ideas to provide supporting evidence for Arveson’s hyperrigidity conjecture. Prompted by various characterizations of hyperrigidity in terms of states, we examine unperforated pairs of self-adjoint subspaces in a ${{\text{C}}^{*}}$-algebra. The configuration of the subspaces forming an unperforated pair is in some sense compatible with the order structure of the ambient ${{\text{C}}^{*}}$-algebra. We prove that commuting pairs are unperforated and obtain consequences for hyperrigidity. Finally, by exploiting recent advances in the tensor theory of operator systems, we show how the weak expectation property can serve as a flexible relaxation of the notion of unperforated pairs.

Let $W$ be a compact simply connected triangulated manifold with boundary and let $K\,\subset \,W$ be a subpolyhedron. We construct an algebraic model of the rational homotopy type of $W\text{ }\!\!\backslash\!\!\text{ K}$ out of a model of the map of pairs $\left( K,\,K\cap \partial W \right)\,\to \,\left( W,\,\partial W \right)$ under some high codimension hypothesis.

We deduce the rational homotopy invariance of the configuration space of two points in a compact manifold with boundary under 2-connectedness hypotheses. Also, we exhibit nice explicit models of these configuration spaces for a large class of compact manifolds.

If the Hasse invariant of a $P$ -divisible group is small enough, then one can construct a canonical subgroup inside its $P$-torsion. We prove that, assuming the existence of a subgroup of adequate height in the $P$-torsion with high degree, the expected properties of the canonical subgroup can be easily proved, especially the relation between its degree and the Hasse invariant. When one considers a $P$-divisible group with an action of the ring of integers of a (possibly ramified) finite extension of ${{\mathbb{Q}}_{P}}$ , then much more can be said. We define partial Hasse invariants (which are natural in the unramified case, and generalize a construction of Reduzzi and Xiao in the general case), as well as partial degrees. After studying these functions, we compute the partial degrees of the canonical subgroup.

The object of this paper is to prove a version of the Beurling–Helson–Lowdenslager invariant subspace theorem for operators on certain Banach spaces of functions on a multiply connected domain in $\mathbb{C}$. The norms for these spaces are either the usual Lebesgue and Hardy space norms or certain continuous gauge norms. In the Hardy space case the expected corollaries include the characterization of the cyclic vectors as the outer functions in this context, a demonstration that the set of analytic multiplication operators is maximal abelian and reflexive, and a determination of the closed operators that commute with all analytic multiplication operators.

We define Schwartz functions, tempered functions, and tempered distributions on (possibly singular) real algebraic varieties. We prove that all classical properties of these spaces, defined previously on affine spaces and on Nash manifolds, also hold in the case of affine real algebraic varieties, and give partial results for the non-affine case.

We will give a representation-theoretic proof for the multiplication formula in the Ringel-Hall algebra $\mathfrak{H}\vartriangle \,(n)$ of a cyclic quiver $\Delta \,(n)$. As a first application, we see immediately the existence of Hall polynomials for cyclic quivers, a fact established by J. Y. Guo and C. M. Ringel, and derive a recursive formula to compute them. We will further use the formula and the construction of a monomial basis for $\mathfrak{H}\vartriangle \,(n)$ given by Deng, Du, and Xiao together with the double Ringel-Hall algebra realisation of the quantum loop algebra ${{U}_{v}}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{n}})$ given by Deng, Du, and Fu to develop some algorithms and to compute the canonical basis for $U_{v}^{+}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{n}})$. As examples, we will show explicitly the part of the canonical basis associated with modules of Lowey length at most 2 for the quantum group ${{U}_{v}}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{2}})$.

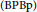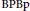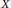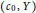We study the Bishop-Phelps-Bollobàs property $\left( \text{BPBp} \right)$ for compact operators. We present some abstract techniques that allow us to carry the $\text{BPBp}$ for compact operators from sequence spaces to function spaces. As main applications, we prove the following results. Let $X$ and $Y$ be Banach spaces. If $\left( {{c}_{0}},Y \right)$ has the 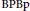$\text{BPBp}$ for compact operators, then so do 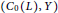$\left( {{C}_{0}}\left( L \right),Y \right)$ for every locally compact Hausdorff topological space $L$ and 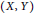$\left( X,\,Y \right)$ whenever 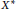${{X}^{*}}$ is isometrically isomorphic to 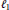${{\ell }_{1}}$. If 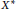${{X}^{*}}$ has the Radon-Nikodým property and 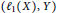$\left( {{\ell }_{1}}\left( X \right),\,Y \right)$ has the 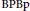$\text{BPBp}$ for compact operators, then so does 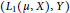$\left( {{L}_{1}}\left( \mu ,X \right),\,\,Y \right)$ for every positive measure $\mu $; as a consequence, 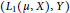$\left( {{L}_{1}}\left( \mu ,X \right),\,\,Y \right)$ has the 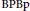$\text{BPBp}$ for compact operators when 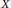$X$ and $Y$ are finite-dimensional or $Y$ is a Hilbert space and 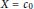$X={{c}_{0}}$ or 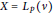$X={{L}_{p}}\left( v \right)$ for any positive measure $v$ and 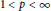$1\,<\,p\,<\,\infty $. For 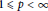$1\,\le p\,<\,\infty$, if 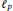$\left( X,{{l}_{p}}(Y) \right)$ has the 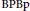$\text{BPBp}$ for compact operators, then so does 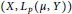$\left( X,{{L}_{p}}\left( \mu ,\,Y \right) \right)$ for every positive measure $\mu $ such that 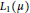${{L}_{1}}\left( \mu \right)$ is infinite-dimensional. If 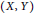$\left( X,\,Y \right)$ has the 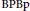$\text{BPBp}$ for compact operators, then so do 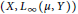$\left( X,\,{{L}_{\infty }}\left( \mu ,\,\,Y \right) \right)$ for every $\sigma $-finite positive measure $\mu $ and 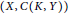$\left( X,\,C\left( K,\,Y \right) \right)$ for every compact Hausdorff topological space 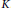$K$.

In this paper we discuss the range of a co-analytic Toeplitz operator. These range spaces are closely related to de Branges–Rovnyak spaces (in some cases they are equal as sets). In order to understand its structure, we explore when the range space decomposes into the range of an associated analytic Toeplitz operator and an identifiable orthogonal complement. For certain cases, we compute this orthogonal complement in terms of the kernel of a certain Toeplitz operator on the Hardy space, where we focus on when this kernel is a model space (backward shift invariant subspace). In the spirit of Ahern–Clark, we also discuss the non-tangential boundary behavior in these range spaces. These results give us further insight into the description of the range of a co-analytic Toeplitz operator as well as its orthogonal decomposition. Our Ahern–Clark type results, which are stated in a general abstract setting, will also have applications to related sub-Hardy Hilbert spaces of analytic functions such as the de Branges–Rovnyak spaces and the harmonically weighted Dirichlet spaces.

This paper constitutes a comprehensive study of ten classes of self-maps on metric spaces $\langle X\,,\,d\rangle $ with the pointwise (i.e., local radial) and local contraction properties. Each of these classes appeared previously in the literature in the context of fixed point theorems.

We begin with an overview of these fixed point results, including concise self contained sketches of their proofs. Then we proceed with a discussion of the relations among the ten classes of self-maps with domains $\langle X\,,\,d\rangle $ having various topological properties that often appear in the theory of fixed point theorems: completeness, compactness, (path) connectedness, rectifiable-path connectedness, and $d$-convexity. The bulk of the results presented in this part consists of examples of maps that show non-reversibility of the previously established inclusions between these classes. Among these examples, the most striking is a differentiable auto-homeomorphism $f$ of a compact perfect subset $X$ of $\mathbb{R}$ with ${{f}^{'}}\,\equiv \,0$, which constitutes also a minimal dynamical system. We finish by discussing a few remaining open problems on whether the maps with specific pointwise contraction properties must have the fixed points.

We address the classification problem for graph ${{C}^{*}}$-algebras of finite graphs (finitely many edges and vertices), containing the class of Cuntz-Krieger algebras as a prominent special case. Contrasting earlier work, we do not assume that the graphs satisfy the standard condition $\left( K \right)$, so that the graph ${{C}^{*}}$-algebras may come with uncountably many ideals.

We find that in this generality, stable isomorphism of graph ${{C}^{*}}$-algebras does not coincide with the geometric notion of Cuntz move equivalence. However, adding a modest condition on the graphs, the two notions are proved to be mutually equivalent and equivalent to the C*-algebras having isomorphic $K$-theories. This proves in turn that under this condition, the graph ${{C}^{*}}$-algebras are in fact classifiable by $K$-theory, providing, in particular, complete classification when the ${{C}^{*}}$- algebras in question are either of real rank zero or type I/postliminal. The key ingredient in obtaining these results is a characterization of Cuntz move equivalence using the adjacency matrices of the graphs.

Our results are applied to discuss the classification problem for the quantumlens spaces defined by Hong and Szymański, and to complete the classification of graph ${{C}^{*}}$-algebras associated with all simple graphs with four vertices or less.

This note provides a correct proof of the result claimed by the second author that locally compact normal spaces are collectionwise Hausdorff in certain models obtained by forcing with a coherent Souslin tree. A novel feature of the proof is the use of saturation of the non-stationary ideal on ${{\omega }_{1}}$, as well as of a strong form of Chang's Conjecture. Together with other improvements, this enables the consistent characterization of locally compact hereditarily paracompact spaces as those locally compact, hereditarily normal spaces that do not include a copy of ${{\omega }_{1}}$.

Order three elements in the exceptional groups of type ${{G}_{2}}$ are classified up to conjugation over arbitrary fields. Their centralizers are computed, and the associated classification of idempotents in symmetric composition algebras is obtained. Idempotents have played a key role in the study and classification of these algebras.

Over an algebraically closed field, there are two conjugacy classes of order three elements in ${{G}_{2}}$ in characteristic not 3 and four of them in characteristic 3. The centralizers in characteristic 3 fail to be smooth for one of these classes.