Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T17:13:43.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Weights of the Mod p Kernels of Theta Operators

Published online by Cambridge University Press:  20 November 2018

Siegfried Böcherer ,
Toshiyuki Kikuta  and
Sho Takemori
Siegfried Böcherer
Affiliation:
Mathematisches Institut, Universität Mannheim, 68131 Mannheim, Germany e-mail: [email protected]
Toshiyuki Kikuta
Affiliation:
Faculty of Information Engineering, Department of Information and Systems Engineering, Fukuoka Institute of Technology, 3-30-1 Wajiro-higashi, Higashi-ku, Fukuoka 811-0295, Japan e-mail: [email protected]
Sho Takemori
Affiliation:
Department of Mathematics, Hokkaido University, Kita 10, Nishi 8, Kita-Ku, Sapporo, 060-0810, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

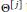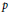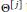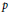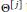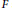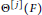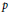Let ${{\Theta }^{[j]}}$ be an analogue of the Ramanujan theta operator for Siegel modular forms. For a given prime $p$ , we give the weights of elements of mod $p$ kernel of ${{\Theta }^{[j]}}$ , where the mod $p$ kernel of ${{\Theta }^{[j]}}$ is the set of all Siegel modular forms $F$ such that ${{\Theta }^{[j]}}(F)$ is congruent to zero modulo $p$ . In order to construct examples of the mod $p$ kernel of 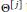${{\Theta }^{[j]}}$ from any Siegel modular forms, we introduce new operators 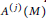${{A}^{(j)}}(M)$ and show the modularity of $F|{{A}^{\left( j \right)}}\left( M \right)$ when 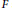$F$ is a Siegel modular form. 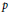Finally, we give some examples of the mod $p$ kernel of 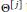${{\Theta }^{[j]}}$ and the filtrations of some of them.

Keywords

11F3311F46Siegel modular formcongruences for modular formsFourier coefficientsRamanujan's operatorfiltration
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 241 - 264
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Andrianov, A. N.and Zhuravlev, V. G., Modular forms and Hecke operators. AMS Translations of Mathematical Monographs 145,1995.Google Scholar
[2] Böcherer, S., Über gewisse Siegelsche Modulformen zweiten Grades. Math. Ann. 261(1982), 23–41.http://dx.doi.Org/10.1007/BF01456406 Google Scholar
[3] Böcherer, S., On the Hecke operator U(p). With an appendix by Ralf Schmidt. J. Math. Kyoto Univ. 45(2005), no. 4, 807–829. http://dx.doi.org/10.1215/kjm/1250281658 Google Scholar
[4] Böcherer, S., and Kikuta, T., On modp singular modular forms. Forum Math. 28(2016), no. 6, 1051–1065.10.1515/forum-2015-0062Google Scholar
[5] Böcherer, S., Kodama, H., and Nagaoka, S., On the kernel of the theta operator modp. Manuscripta Math., to appear. http://arxiv:1707.03680 Google Scholar
[6] Böcherer, S. and Nagaoka, S., On mod p properties of Siegel modular forms. Math. Ann. 338(2007), 421–433. http://dx.doi.org/10.1007/s00208-007-0081-7 Google Scholar
[7] Böcherer, S. and Nagaoka, S., Congruences for Siegel modular forms and their weights. Abh. Math. Semin. Univ. Hambg. 80(2010), 227–231.http://dx.doi.Org/10.1007/s12188-010-0042-z Google Scholar
[8] Böcherer, S. and Nagaoka, S., On p-adic properties ofSiegel modular forms. In: Automorphic forms. Springer Proc. Math. Stat , 115. Springer, Cham, 2014, pp. 47–66.Google Scholar
[9] Choi, D., Choie, Y., and Kikuta, T., Sturm type theorem for Siegel modular forms of genus 2 modulo p. Acta Arith. 158(2013), no. 2, 129–139.http://dx.doi.Org/10.4064/aa158-2-2 Google Scholar
[10] Choi, D., Choie, Y., and Richter, O., Congruences for Siegel modular forms. Annales de l'Institut Fourier , 61(2011) no.4, 1455–1466, http://dx.doi.org/10.5802/aif.2646 Google Scholar
[11] Dewar, M. and Richter, O., Ramanujan congruences for Siegel modular forms. Int. J. Number Theory 6(2010), no. 7, 1677–1687 http://dx.doi.Org/10.1142/S179304211000371X Google Scholar
[12] Eichler, M. and Zagier, D., The theory of facobi forms. Progress in Mathematics , 55. Birkhäuser, Boston, 1985.Google Scholar
[13] Freitag, E., Siegekche Modulfunktionen. Grundlehren der Mathematischen Wissenschaften , 254. Springer-Verlag, Berlin, 1983.Google Scholar
[14] Ichikawa, T., Congruences between Siegel modular forms. Math. Ann. 342(2008), no. 3, 527–532. http://dx.doi.Org/10.1007/s00208-008-0245-0 Google Scholar
[15] Katz, N. M., A result on modular forms in characteristic p. Modular functions of one variable, V. Lecture Notes in Math. , 601, Springer, Berlin, 1977, pp. 53–61.Google Scholar
[16] Kikuta, T., Kodama, H., and Nagaoka, S., Note on Igusa's cusp form of weight 35. Rocky Mountain J. Math. 45(2015), no. 3, 963–972.http://dx.doi.org/10.1216/RMJ-2015-45-3-963 Google Scholar
[17] Kikuta, T. and Takemori, S., Sturm bounds for Siegel modular forms of degree 2 and odd weights. http://arxiv:1 508.01 610 Google Scholar
[18] Mizumoto, S., On integrality of certain algebraic numbers associated with modular forms. Math. Ann. 265(1983), no. 1, 119–135.http://dx.doi.org/10.1007/BF01456941 Google Scholar
[19] Nagaoka, S., Note on mod p Siegel modular forms. Mathe Zeitschrift 235(2000), no. 2, 405–420. http://dx.doi.Org/10.1007/s002090000135 Google Scholar
[20] Nagaoka, S., Note on mod p Siegel modular forms. II. Mathe Zeitschrift 251(2005), no. 4, 821–826.http://dx.doi.org/10.1007/s00209-005-0832-7 Google Scholar
[21] Nagaoka, S., On the mod p kernel of the theta operator. Proc. Amer. Math. Soc. 143(2015), no. 10, 4237–4244.http://dx.doi.org/10.1090/S0002-9939-2015-12567-1 Google Scholar
[22] Nagaoka, S. and Takemori, S., Notes on theta series for Niemeier lattices. Ramanujan J. 42(2017), no. 2, 385–400.http://dx.doi.Org/10.1007/s11139-015-9720-x Google Scholar
[23] Serre, J.-P., Formes modulaires et fonctions zêta p-adiques. In: Modular functions of one variable, III. Lecture Notes in Math. , 350. Springer, Berlin, 1973, pp. 191–268.10.1007/978-3-540-37802-0_4Google Scholar
[24] Swinnerton-Dyer, H. P. F., On l-adic representations and congruences for coefficients of modular forms. In: Modular functions of one variable, III. Lecture Notes in Math. , 350. Springer, Berlin, 1973, pp. 1–55.10.1007/978-3-540-37802-0_1Google Scholar
[25] Takemori, S., Congruence relations for Siegel modular forms of weight 47, 71, and 89. Exp. Math. 23(2014), no. 4, 423–428.http://dx.doi.org/10.1080/10586458.2014.935895 Google Scholar
[26] Weissauer, R., Siegel modular forms mod p. http://arxiv:0804.3134 Google Scholar
[27] Weissauer, R., Vektorwertige Siegelsche Modulformen kleinen Gewichtes. J. Reine Angew. Math. 343(1983), 184–202.Google Scholar
[28] Yamauchi, T., The weight reduction of mod p Siegel modular forms for GSpn. http://arxiv:1410.7894 Google Scholar
[29] Ziegler, C., Jacobi forms of higher degree. Abh. Math. Sem. Univ. Hamburg 59(1989), 191–224. http://dx.doi.org/10.1007/BF02942329 Google Scholar