Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T13:04:12.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Unperforated Pairs of Operator Spaces and Hyperrigidity of Operator Systems

Published online by Cambridge University Press:  20 November 2018

Raphaël Clouâtre
Raphaël Clouâtre*
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg R3T 2N2, Manitoba, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study restriction and extension properties for states on 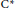${{\text{C}}^{*}}$-algebras with an eye towards hyperrigidity of operator systems. We use these ideas to provide supporting evidence for Arveson’s hyperrigidity conjecture. Prompted by various characterizations of hyperrigidity in terms of states, we examine unperforated pairs of self-adjoint subspaces in a 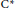${{\text{C}}^{*}}$-algebra. The configuration of the subspaces forming an unperforated pair is in some sense compatible with the order structure of the ambient 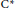${{\text{C}}^{*}}$-algebra. We prove that commuting pairs are unperforated and obtain consequences for hyperrigidity. Finally, by exploiting recent advances in the tensor theory of operator systems, we show how the weak expectation property can serve as a flexible relaxation of the notion of unperforated pairs.

Keywords

46L0746L3046L52operator systemstatepeak pointhyperrigidity conjecture
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 6 , 01 December 2018 , pp. 1236 - 1260
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Altomare, F., Korovkin-type theorems and approximation by positive linear operators. Surv. Approx. Theory 5 (2010), 92–164.Google Scholar
[2] Archbold, R. J., Extensions of pure states and projections of norm one. II. Bull. London Math. Soc. 33 (2001), no. 1, 67–72. http://dx.doi.Org/10.1112/blms/33.1.67Google Scholar
[3] Arveson, W., Subalgebras of C* -algebras. Acta Math. 123 (1969), 141–224. http://dx.doi.org/10.1007/BF02392388Google Scholar
[4] Arveson, W., Subalgebras of C*-algebras. II. Acta Math. 128 (1972), no. 3-4, 271–308. http://dx.doi.Org/10.1007/BF02392166Google Scholar
[5] Arveson, W., An invitation to C*-algebras. Graduate Texts in Mathematics, 39, Springer-Verlag, New York-Heidelberg, 1976.Google Scholar
[6] Arveson, W., The noncommutative Choquet boundary. J. Amer. Math. Soc. 21 (2008), no. 4,1065-1084. http://dx.doi.Org/10.1090/S0894-0347-07-00570-XGoogle Scholar
[7] Arveson, W., The noncommutative Choquet boundary II: hyperrigidity. Israel J. Math. 184 (2011), 349–385. http://dx.doi.Org/10.1007/s11856-011-0071-zGoogle Scholar
[8] Bishop, E. and de Leeuw, K., The representations of linear functionals by measures on sets of extreme points. Ann. Inst. Fourier. Grenoble 9 (1959), 305–331.Google Scholar
[9] Blecher, D. P., The Shilov boundary of an operator space and the characterization theorems. J. Funct. Anal. 182 (2001), no. 2, 280–343. http://dx.doi.Org/10.1006/jfan.2000.3734Google Scholar
[10] Brown, N. P. and Ozawa, N., C*-algebras and finite-dimensional approximations. Graduate Studies in Mathematics, 88, American Mathematical Society, Providence, RI, 2008. http://dx.doi.Org/10.1090/gsm/088Google Scholar
[11] Choi, M. D. and Effros, E. G., Injectivity and operator spaces. J. Functional Analysis 24 (1977), no. 2, 156–209.Google Scholar
[12] Clouâtre, R. and Hartz, M., Multiplier algebras of complete Nevanlinna-Pick spaces: dilations, boundary representations and hyperrigidity. J. Funct. Anal. 274 (2018) no. 6, 1690–1738. http://dx.doi.Org/10.1016/j.jfa.2O17.10.008Google Scholar
[13] Clouâtre, R. and Ramsey, C., A completely bounded non-commutative Choquet boundary for operator spaces. Int. Math. Res. Not. IMRN, rnx335. http://dx.doi.Org/10.1093/imrn/rnx335Google Scholar
[14] Davidson, K. R. and Kennedy, M., The Choquet boundary of an operator system. Duke Math. J. 164 (2015), no. 15, 2989–3004. http://dx.doi.org/10.1215/00127094-3165004Google Scholar
[15] Davidson, K. R. and Kennedy, M., Choquet order and hyperrigidity for function systems. 2016. arxiv:1608.02334Google Scholar
[16] Dixmier, J., C*-algebras. North-Holland Mathematical Library, 15, North-Holland Publishing Co., Amsterdam-New York-Oxford, 1977.Google Scholar
[17] Dritschel, M. A. and McCullough, S. A., Boundary representations for families of representations of operator algebras and spaces. J. Operator Theory 53 (2005), no. 1, 159–167.Google Scholar
[18] Farenick, D. R., Extremal matrix states on operator systems. J. London Math. Soc. (2) 61 (2000), no. 3, 885-892. http://dx.doi.Org/10.1112/S0024610799008613Google Scholar
[19] Fuller, A. H., Hartz, M., and Lupini, M., Boundary representations of operator spaces, and compact rectangular matrix convex sets. 2016. arxiv:1610.05828Google Scholar
[20] Gamelin, T. W., Uniform algebras. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1969.Google Scholar
[21] Hamana, M., Injective envelopes of operator systems, Publ. Res. Inst. Math. Sci. 15 (1979), no. 3, 773–785. http://dx.doi.org/10.2977/prims/1195187876Google Scholar
[22] article M. Hamana, Triple envelopes and Silov boundaries of operator spaces. Math. J. Toyama Univ. 22 (1999), 77–93.Google Scholar
[23] Hamhalter, J., Multiplicativity of extremal positive maps on abelian parts of operator algebras. J. Operator Theory 48 (2002), no. 2, 369–383.Google Scholar
[24] Kadison, R. V. and Singer, I. M., Extensions of pure states. Amer. J. Math. 81 (1959), 383–400. http://dx.doi.Org/10.2307/2372748Google Scholar
[25] Kavruk, A. S., The Weak expectation property and Riesz interpolation. 2012. arxiv:1201.5414Google Scholar
[26] Kennedy, M. and Shalit, O. M., Essential normality, essential norms and hyperrigidity. J. Funct. Anal. 268 (2015), no. 10, 2990–3016. http://dx.doi.Org/10.1016/j.jfa.2015.03.014Google Scholar
[27] Kleski, C., Korovkin-type properties for completely positive maps. Illinois J. Math. 58 (2014), no. 4, 1107–1116.Google Scholar
[28] Korovkin, P. P., On convergence of linear positive operators in the space of continuous functions. (Russian) Doklady Akad. Nauk SSSR (N.S.) 90 (1953), 961–964.Google Scholar
[29] Lance, C., On nuclear C*-algebras. J. Functional Analysis 12 (1973), 157–176. http://dx.doi.Org/10.1016/0022-1236(73)90021-9Google Scholar
[30] Marcus, A. W., Spielman, D. A., and Srivastava, N., Interlacing families II: Mixed characteristic polynomials and the Kadison-Singer problem. Ann. of Math. (2) 182 (2015), no. 1, 327–350. http://dx.doi.Org/10.4007/annals.2015.1 82.1.8Google Scholar
[31] Muhly, P. S. and Solel, B., An algebraic characterization of boundary representations. In: Nonselfadjoint operator algebras, operator theory, and related topics, Oper. Theory Adv. Appl., 104, Birkhâuser, Basel, 1998, pp. 189–196.Google Scholar
[32] Namboodiri, M. N. N., Pramod, S., Shankar, P., and Vijayarajan, A. K., Quasi hyperrigidity and weak peak points for non-commutative operator systems. 2016. arxiv:161O.O2165Google Scholar
[33] Paulsen, V., Completely bounded maps and operator algebras. Cambridge Studies in Advanced Mathematics, 78, Cambridge University Press, Cambridge, 2002.Google Scholar
[34] Phelps, R. R., Lectures on Choquet's theorem. Second éd., Lecture Notes in Mathematics, 1757, Springer-Verlag, Berlin, 2001. http://dx.doi.Org/10.1007/b76887Google Scholar
[35] Rudin, W., Function theory in the unit ball ofC”. Classics in Mathematics, Springer-Verlag, Berlin, 2008.Google Scholar
[36] SzNagy, B., Foias, C., Bercovici, H., and Kérchy, L., Harmonic analysis of operators on Hilbert space. Universitext, Springer, New York, 2010. http://dx.doi.org/10.1007/978-1-4419-6094-8Google Scholar
[37] Saskin, J. A., The MH'man-Choquet boundary and the theory of approximations. Funkcional. Anal. i Prilozen. 1 (1967), no. 2, 95–96.Google Scholar
[38] Webster, C. and Winkler, S., The Krein-Milman theorem in operator convexity. Trans. Amer. Math. Soc. 351 (1999), no. 1, 307–322. http://dx.doi.org/10.1090/S0002-9947-99-02364-8Google Scholar