In the present paper a concept of topological essentiality for a large class of multivalued mappings is introduced. This concept is strictly related to the Leray-Schauder topological degree theory but is simpler and also more general. Applying the above concept to boundary value problems for differential inclusion with both upper semi-continuous and lower semi-continuous right hand sides, several new results are obtained.

This paper discusses rational edged tetrahedra, in 3, 4 and n dimensions, with rational volume. The main results are (i) a proof of the existence of infinitely many tetrahedra with rational edge-lengths, face-areas and volume and (ii) a proof that there exist dimensions for which all regular hypertetrahedra with rational edge-lengths have rational hypervolume.

The abelian groups that can be written as a union of proper subgroups are characterised, all the ways that this can be done for a given group are indicated, and the minimal number of subgroups necessary for such a decomposition of a given group is determined.

Let A be the class of functions f(z) which are analytic in the unit disk U with f(0) = f′(0) - 1 = 0. A subclass S(λ, M) (λ > 0, M > 0) of A is introduced. The object of the present paper is to prove some interesting convolution properties of functions f(z) belonging to the class S(λ, M). Also a certain integral operator J for f(z) in the class A is considered.

Consider the following neutral delay differential equation

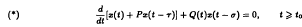
where P ∈ ℝ, T ∈ (0, ∞), σ ∈ (0, ∞) and Q ∈ C[(t0, ∞), [0, ∞)]. We obtain a sufficient condition for the oscillation of all solutions of Equation (*) with P = −1, which does not require that

But, for the cases −1 < P < 0 and P < −1, we show that (**) is a necessary condition for the oscillation of all solutions of Equation (*). These new results solve some open problems in the literature.

We study a concept of stability under the gap of isomorphic properties of Banach spaces and apply it to obtain some results of stability under compact or small norm perturbation for non-semi-Fredholm operators with closed range.

Let X be a real uniformly convex Banach space satisfying the Opial's condition, C a bounded closed convex subset of X, and T: C → C an asymptotically non-expansive mapping. Then we show that for each x in C, the sequence {Tnx} almost converges weakly to a fixed point y of T, that is,

This implies that {Tnx} converges weakly to y if and only if T is weakly asymptotically regular at x, that is, weak- . We also present a weak convergence theorem for asymptotically nonexpansive semigroups.

It is shown that the set of all orthodox subsemigroups of an orthodox semigroup forms a lattice. This lattice is a join-sublattice of the lattice of all semigroups, but is not in general a meet-sublattice. We obtain results concerning lattice isomorphisms between orthodox semigroups, several of which include known results for inverse semigroups as special cases.

We consider twists of matrix algebras by some continuous characters. There are some subgroups of Brauer groups arising from these twists. Some results regarding these subgroups are proved.

We give a formula on the ε−subdifferential of the difference of two convex functions. As a by-product of this formula, one recovers a recent result of Hiriart-Urruty, namely, a necessary and sufficient condition for global optimality in nonconvex optimisation.

In this paper, we shall prove a generalisation of Himmelberg's fixed point theorem and as applications, the existence of equilibrium points for abstract economies given by preference correspondences and utility functions have been established.

We show that trigonometric Lagrange interpolating approximation with arbitrary real distinct nodes in Lp space for 1 ≤ p < ∞, as that with equally spaced nodes in Lp space for 1 < p < ∞ in an earlier paper by T.F. Xie and S.P. Zhou, may also be arbitrarily “bad”. This paper is a continuation of this earlier work by Xie and Zhou, but uses a different method.

In this paper we have evaluated the integral . A new integral representation of the Euler constant is shown. Some special cases of the result are discussed and an open problem is posed.

Fefferman has proved that the dual space of the martingale Hardy space H1 is the BMO1-space. Garsia went further and proved that the dual of Hp is the so-called martingale Kp-space, where p and q are two conjugate numbers and 1 ≤ p < 2.

The martingale Hardy spaces HΦ with general Young function Φ, were investigated by Bassily and Mogyoródi. In this paper we show that the dual of the martingale Hardy space HΦ is the martingale Hardy space HΦ where (Φ, Ψ) is a pair of conjugate Young functions such that both Φ and Ψ have finite power. Moreover, two other remarkable dualities are presented.

The set functions associated with Schrödinger's equation are known to be unbounded on the algebra of cylinder sets. However, there do exist examples of scalar valued set functions which are unbounded, yet σ-additive on the underlying algebra of sets. The purpose of this note is to show that the set functions associated with Schrödinger's equation are not σ-additive on cylinder sets. In the course of the proof, general conditions implying the non-σ-additivity of unbounded set functions are given.

The consideration of compact right topological groups goes back at least to a paper of Ellis in 1958, where it is shown that a flow is distal if and only if the enveloping semigroup of the flow is such a group (now called the Ellis group of the distal flow). Later Ellis, and also Namioka, proved that a compact right topological group admits a left invariant probability measure. As well, Namioka proved that there is a strong structure theorem for compact right topological groups. More recently, John Pym and the author strengthened this structure theorem enough to be able to establish the existence of Haar measure on a compact right topological group, a probability measure that is invariant under all continuous left and right translations, and is unique as such. Examples of compact right topological groups have been considered earlier. In the present paper, we give concrete representations of several Ellis groups coming from low dimensional nilpotent Lie groups. We study these compact right topological groups, and two others, in some detail, paying attention in particular to the structure theorem and Haar measure, and to the question: is Haar measure uniquely determined by left invariance alone? (It is uniquely determined by right invariance alone.) To assist in answering this question, we develop some sufficient conditions for a positive answer. We suspect that one of the examples, a compact right topological group coming from the Euclidean group of the plane, does not satisfy these conditions; we don't know if the question has a positive answer for this group.

The minimum area a(v) of a v–sided convex lattice polygon is known to satisfy . We conjecture that a(v) = cv3 + o(v3), for c a constant; we prove that , and that for some positive constant c, .

We prove a high order conical inverse mapping theorem for set-valued maps on complete metric spaces. An application to a control problem is provided.

A construction method for group divisible designs is employed to construct (i) infinitely many non-symmetric semiregular group divisible designs whose duals are semiregular group divisible designs, and (ii) infinitely many transversal designs whose duals are group divisible 3-associate designs. A construction method for affine α−resolvable balanced incomplete block designs is also given and illustrated.

We provide sufficient convergence conditions as well as sharp error bounds for Newton-like iterations which generalise a wide class of known methods for solving nonlinear equations in Banach space.