Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Reynolds, Robert
and
Stauffer, Allan
2021.
Quadruple Integral Involving the Logarithm and Product of Bessel Functions Expressed in Terms of the Lerch Function.
Axioms,
Vol. 10,
Issue. 4,
p.
324.


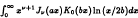 . A new integral representation of the Euler constant is shown. Some special cases of the result are discussed and an open problem is posed.
. A new integral representation of the Euler constant is shown. Some special cases of the result are discussed and an open problem is posed.