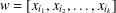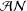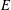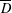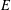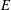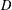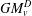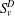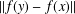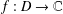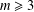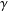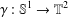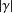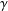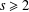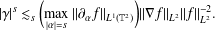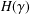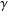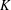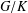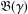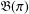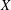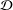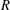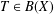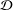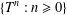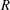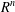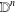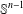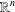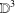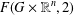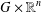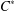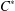Research Article
A NILPOTENCY CRITERION FOR SOME VERBAL SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 281-289
-
- Article
-
- You have access
- Export citation
SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES
- Part of:
-
- Published online by Cambridge University Press:
- 20 March 2019, pp. 109-118
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF TRACIALLY NUCLEAR C*-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 119-128
-
- Article
-
- You have access
- Export citation
BOUNDARY SCHWARZ LEMMA FOR SOLUTIONS TO NONHOMOGENEOUS BIHARMONIC EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2019, pp. 470-478
-
- Article
-
- You have access
- Export citation
A NOTE ON THE PERIODICITY OF ENTIRE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 290-296
-
- Article
-
- You have access
- Export citation
A NOTE ON POSITIVE
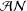 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 129-130
-
- Article
-
- You have access
- Export citation
EXTENDABLE TEMPERATURES
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 297-303
-
- Article
-
- You have access
- Export citation
ESSENTIAL AMENABILITY OF DUAL BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2019, pp. 479-488
-
- Article
-
- You have access
- Export citation
A SYSTEM OF FUNCTIONAL EQUATIONS SATISFIED BY COMPONENTS OF A QUADRATIC FUNCTION AND ITS STABILITY
-
- Published online by Cambridge University Press:
- 27 February 2019, pp. 304-316
-
- Article
-
- You have access
- Export citation
LIPSCHITZ-TYPE INEQUALITIES FOR ANALYTIC FUNCTIONS IN BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 489-497
-
- Article
-
- You have access
- Export citation
INTEGER POLYGONS OF GIVEN PERIMETER
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. 131-147
-
- Article
-
- You have access
- Export citation
A COMPACTNESS PRINCIPLE FOR MAXIMISING SMOOTH FUNCTIONS OVER TOROIDAL GEODESICS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 148-154
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE FROBENIUS RECIPROCITY THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2019, pp. 317-322
-
- Article
-
- You have access
- Export citation
NEW COUNTEREXAMPLES ON RITT OPERATORS, SECTORIAL OPERATORS AND
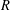 $R$-BOUNDEDNESS
$R$-BOUNDEDNESS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 498-506
-
- Article
-
- You have access
- Export citation
A NOTE ON RADIAL SYMMETRY FOR AN INTEGRAL EQUATION OF WOLFF TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2019, pp. 323-327
-
- Article
-
- You have access
- Export citation
SPACES OF SPECIAL QUADRILATERALS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 155-167
-
- Article
-
- You have access
- Export citation
CATEGORY AND TOPOLOGICAL COMPLEXITY OF THE CONFIGURATION SPACE
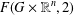 $F(G\times \mathbb{R}^{n},2)$
$F(G\times \mathbb{R}^{n},2)$
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2019, pp. 507-517
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
WEAK SUBORDINATION OF MULTIVARIATE LÉVY PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 518-519
-
- Article
-
- You have access
- Export citation
GEOMETRY OF INTEGRABLE LATTICE EQUATIONS AND THEIR REDUCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 168-169
-
- Article
-
- You have access
- Export citation
Research Article
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
-
- Article
-
- You have access
- Export citation