Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T06:07:30.309Z Has data issue: false hasContentIssue false
  • English
  • Français

A COMPACTNESS PRINCIPLE FOR MAXIMISING SMOOTH FUNCTIONS OVER TOROIDAL GEODESICS

Part of: Classical measure theory Variational problems in infinite-dimensional spaces Global differential geometry

Published online by Cambridge University Press:  01 February 2019

STEFAN STEINERBERGER Open the ORCID record for STEFAN STEINERBERGER [Opens in a new window]
STEFAN STEINERBERGER*
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06511, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 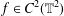$f\in C^{2}(\mathbb{T}^{2})$ have mean value 0 and consider

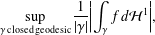$$\begin{eqnarray}\sup _{\unicode[STIX]{x1D6FE}\,\text{closed geodesic}}\frac{1}{|\unicode[STIX]{x1D6FE}|}\biggl|\int _{\unicode[STIX]{x1D6FE}}f\,d{\mathcal{H}}^{1}\biggr|,\end{eqnarray}$$
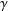where $\unicode[STIX]{x1D6FE}$ ranges over all closed geodesics 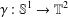$\unicode[STIX]{x1D6FE}:\mathbb{S}^{1}\rightarrow \mathbb{T}^{2}$ and $|\unicode[STIX]{x1D6FE}|$ denotes its length. We prove that this supremum is always attained. Moreover, we can bound the length of the geodesic 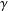$\unicode[STIX]{x1D6FE}$ attaining the supremum in terms of the smoothness of the function: for all 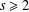$s\geq 2$,
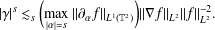$$\begin{eqnarray}|\unicode[STIX]{x1D6FE}|^{s}{\lesssim}_{s}\biggl(\max _{|\unicode[STIX]{x1D6FC}|=s}\Vert \unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FC}}f\Vert _{L^{1}(\mathbb{T}^{2})}\biggr)\Vert \unicode[STIX]{x1D6FB}f\Vert _{L^{2}}\Vert f\Vert _{L^{2}}^{-2}.\end{eqnarray}$$

Keywords

closed geodesicsmaximisationrigidity

MSC classification

Primary: 53C22: Geodesics
Secondary: 28A75: Length, area, volume, other geometric measure theory 58E10: Applications to the theory of geodesics (problems in one independent variable)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 148 - 154
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is supported by the NSF (DMS-1763179) and the Alfred P. Sloan Foundation.

References

Berger, M., A Panoramic View of Riemannian Geometry (Springer, Berlin, 2003).10.1007/978-3-642-18245-7Google Scholar
Grafakos, L., Classical Fourier Analysis, 2nd edn, Graduate Texts in Mathematics, 249 (Springer, Berlin–New York, 2008).Google Scholar
Klingenberg, W., Lectures on Closed Geodesics, Grundlehren der mathematischen Wissenschaften, 230 (Springer, Berlin–New York, 1978).Google Scholar