Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-08T23:44:39.629Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW COUNTEREXAMPLES ON RITT OPERATORS, SECTORIAL OPERATORS AND 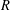$R$-BOUNDEDNESS

Part of: Groups and semigroups of linear operators, their generalizations and applications General theory of linear operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  11 April 2019

LORIS ARNOLD  and
CHRISTIAN LE MERDY Open the ORCID record for CHRISTIAN LE MERDY [Opens in a new window]
LORIS ARNOLD
Affiliation:
Laboratoire de Mathématiques de Besançon, UMR 6623, CNRS, Université Bourgogne Franche-Comté, 25030 Besançon Cedex, France email [email protected]
CHRISTIAN LE MERDY*
Affiliation:
Laboratoire de Mathématiques de Besançon, UMR 6623, CNRS, Université Bourgogne Franche-Comté, 25030 Besançon Cedex, France email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 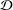${\mathcal{D}}$ be a Schauder decomposition on some Banach space 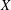$X$. We prove that if 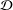${\mathcal{D}}$ is not 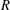$R$-Schauder, then there exists a Ritt operator 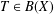$T\in B(X)$ which is a multiplier with respect to 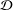${\mathcal{D}}$ such that the set 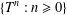$\{T^{n}:n\geq 0\}$ is not 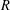$R$-bounded. Likewise, we prove that there exists a bounded sectorial operator 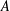$A$ of type 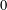$0$ on 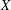$X$ which is a multiplier with respect to 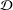${\mathcal{D}}$ such that the set 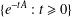$\{e^{-tA}:t\geq 0\}$ is not 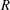$R$-bounded.

Keywords

sectorial operatorsRitt operatorsR-boundedness

MSC classification

Primary: 47D03: Groups and semigroups of linear operators
Secondary: 46B15: Summability and bases 47A99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 498 - 506
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors were supported by the French ‘Investissements d’Avenir’ program, project ISITE-BFC (contract ANR-15-IDEX-03).

References

Arnold, L., ‘ $\unicode[STIX]{x1D6FE}$ -boundedness of $C_{0}$ -semigroups and their $H^{\infty }$ -functional calculi’, Preprint, 2018.Google Scholar
Baillon, J.-B. and Clément, P., ‘Examples of unbounded imaginary powers of operators’, J. Funct. Anal. 100(2) (1991), 419–434.Google Scholar
Blunck, S., ‘Maximal regularity of discrete and continuous time evolution equations’, Studia Math. 146(2) (2001), 157–176.Google Scholar
Fackler, S., ‘The Kalton–Lancien theorem revisited: maximal regularity does not extrapolate’, J. Funct. Anal. 266 (2014), 121–138.Google Scholar
Hytönen, T., van Neerven, J., Veraar, M. and Weis, L., Analysis in Banach Spaces, Vol. II, Results in Mathematics and Related Areas, 3rd Series, A Series of Modern Surveys in Mathematics, 67 (Springer, Cham, 2017).Google Scholar
Kalton, N., Kunstmann, P. and Weis, L., ‘Perturbations and interpolation theorems for H ∞ -calculus with applications to differential operators’, Math. Ann. 336 (2006), 747–801.Google Scholar
Kalton, N. and Lancien, G., ‘A solution to the problem of L p-maximal regularity’, Math. Z. 235(3) (2000), 559–568.Google Scholar
Kunstmann, P. and Weis, L., ‘Maximal L p-regularity for parabolic equations, Fourier multiplier theorems and H ∞ -functional calculus’, in: Functional Analytic Methods for Evolution Equations, Lecture Notes in Mathematics, 1855 (Springer, Berlin, 2004), 65–311.Google Scholar
Lancien, F. and Le Merdy, C., ‘On functional calculus properties of Ritt operators’, Proc. Roy. Soc. Edinburgh Sect. A 145(6) (2015), 1239–1250.Google Scholar
Lancien, G., ‘Counterexamples concerning sectorial operators’, Arch. Math. (Basel) 71(5) (1998), 388–398.Google Scholar
Le Merdy, C., ‘𝛾-bounded representations of amenable groups’, Adv. Math. 224(4) (2010), 1641–1671.Google Scholar
Le Merdy, C., ‘ H ∞ -functional calculus and square function estimates for Ritt operators’, Rev. Mat. Iberoam. 30(4) (2014), 1149–1190.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces I, Ergebnisse der Mathematik und ihrer Grenzgebiete, 92 (Springer, Berlin–New York, 1977).Google Scholar
Portal, P., ‘Discrete time analytic semigroups and the geometry of Banach spaces’, Semigroup Forum 67(1) (2003), 125–144.Google Scholar
Venni, A., ‘A counterexample concerning imaginary powers of linear operators’, in: Functional analysis and related topics, Kyoto, 1991, Lecture Notes in Mathematics, 1540 (Springer, Berlin, 1993), 381–387.Google Scholar
Weis, L., ‘Operator-valued Fourier multiplier theorems and maximal L p-regularity’, Math. Ann. 319(4) (2001), 735–758.Google Scholar