Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-03T18:30:19.167Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS

Part of: Normed linear spaces and Banach spaces; Banach lattices Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  07 February 2019

TATIANA SHULMAN Open the ORCID record for TATIANA SHULMAN [Opens in a new window]  and
OTGONBAYAR UUYE Open the ORCID record for OTGONBAYAR UUYE [Opens in a new window]
TATIANA SHULMAN
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland email [email protected]
OTGONBAYAR UUYE*
Affiliation:
Institute of Mathematics, National University of Mongolia, Ikh Surguuliin Gudamj 1, Sukhbaatar District, Ulaanbaatar, Mongolia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

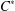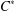Let $n$ be a positive integer. A $C^{\ast }$-algebra is said to be $n$-subhomogeneous if all its irreducible representations have dimension at most $n$. We give various approximation properties characterising $n$-subhomogeneous $C^{\ast }$-algebras.

Keywords

subhomogeneous algebraC∗ -algebrafinite-dimensional algebracompletely positivecompletely contractive

MSC classification

Primary: 46B28: Spaces of operators; tensor products; approximation properties
Secondary: 46L07: Operator spaces and completely bounded maps 47L30: Abstract operator algebras on Hilbert spaces 47L55: Representations of (nonselfadjoint) operator algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 328 - 337
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by a Polish National Science Centre grant under the contract number DEC2012/06/A/ST1/00256 and by the grant H2020-MSCA-RISE-2015-691246-QUANTUM DYNAMICS. The second author was supported by Mongolian Science and Technology Foundation grants SSA-012/2016 and ShuSs-2017/76.

References

Blackadar, B., Operator Algebras: Theory of C ∗ -Algebras and von Neumann Algebras, Encyclopaedia of Mathematical Sciences, 122 [Operator Algebras and Non-commutative Geometry III] (Springer, Berlin, 2006).Google Scholar
Brown, N. P. and Ozawa, N., C ∗ -Algebras and Finite-dimensional Approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Choi, M. D., ‘Positive linear maps on C ∗ -algebras’, Canad. J. Math. 24 (1972), 520–529.Google Scholar
De Cannière, J. and Haagerup, U., ‘Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups’, Amer. J. Math. 107(2) (1985), 455–500.10.2307/2374423Google Scholar
Huruya, T. and Tomiyama, J., ‘Completely bounded maps of C ∗ -algebras’, J. Operator Theory 10(1) (1983), 141–152.Google Scholar
Loebl, R. I., ‘Contractive linear maps on C ∗ -algebras’, Michigan Math. J. 22(4) (1976), 361–366.Google Scholar
Pedersen, G. K., C ∗ -Algebras and Their Automorphism Groups, London Mathematical Society Monographs, 14 (Academic Press [Harcourt Brace Jovanovich], London, 1979).Google Scholar
Smith, R. R., ‘Completely bounded maps between C ∗ -algebras’, J. Lond. Math. Soc. (2) 27(1) (1983), 157–166.10.1112/jlms/s2-27.1.157Google Scholar
Smith, R. R., ‘Completely contractive factorizations of C ∗ -algebras’, J. Funct. Anal. 64(3) (1985), 330–337.Google Scholar
Stinespring, W. F., ‘Positive functions on C ∗ -algebras’, Proc. Amer. Math. Soc. 6 (1955), 211–216.Google Scholar
Takesaki, M., Theory of Operator Algebras. I, Encyclopaedia of Mathematical Sciences, 124 (Springer, Berlin, 2002), reprint of the first (1979) edition.Google Scholar
Tomiyama, J., ‘On the difference of n-positivity and complete positivity in C ∗ -algebras’, J. Funct. Anal. 49(1) (1982), 1–9.Google Scholar
Tomiyama, J. and Takesaki, M., ‘Applications of fibre bundles to the certain class of C ∗ -algebras’, Tôhoku Math. J. (2) 13 (1961), 498–522.Google Scholar
Walter, M. E., ‘Algebraic structures determined by 3 by 3 matrix geometry’, Proc. Amer. Math. Soc. 131(7) (2003), 2129–2131 (electronic).Google Scholar