Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T01:07:58.434Z Has data issue: false hasContentIssue false
  • English
  • Français

A GENERALISATION OF THE FROBENIUS RECIPROCITY THEOREM

Part of: Locally compact groups and their algebras Abstract harmonic analysis

Published online by Cambridge University Press:  18 February 2019

H. KUMUDINI DHARMADASA Open the ORCID record for H. KUMUDINI DHARMADASA [Opens in a new window]  and
WILLIAM MORAN Open the ORCID record for WILLIAM MORAN [Opens in a new window]
H. KUMUDINI DHARMADASA*
Affiliation:
Discipline of Mathematics, School of Natural Sciences, College of Science and Engineering, University of Tasmania, Hobart, Tasmania 7001, Australia email [email protected]
WILLIAM MORAN
Affiliation:
Room 2.29 Building 193, Electrical and Electronic Engineering, The University of Melbourne, Victoria 3010, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 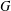$G$ be a locally compact group and 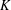$K$ a closed subgroup of 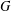$G$. Let 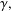$\unicode[STIX]{x1D6FE},$$\unicode[STIX]{x1D70B}$ be representations of 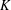$K$ and 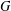$G$ respectively. Moore’s version of the Frobenius reciprocity theorem was established under the strong conditions that the underlying homogeneous space 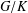$G/K$ possesses a right-invariant measure and the representation space 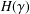$H(\unicode[STIX]{x1D6FE})$ of the representation 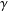$\unicode[STIX]{x1D6FE}$ of 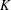$K$ is a Hilbert space. Here, the theorem is proved in a more general setting assuming only the existence of a quasi-invariant measure on 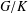$G/K$ and that the representation spaces 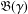$\mathfrak{B}(\unicode[STIX]{x1D6FE})$ and 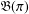$\mathfrak{B}(\unicode[STIX]{x1D70B})$ are Banach spaces with 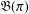$\mathfrak{B}(\unicode[STIX]{x1D70B})$ being reflexive. This result was originally established by Kleppner but the version of the proof given here is simpler and more transparent.

Keywords

separable locally compact groupquasi-invariant measuremodular function𝜆- function

MSC classification

Primary: 43A65: Representations of groups, semigroups, etc.
Secondary: 22D30: Induced representations 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 317 - 322
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Dharmadasa, H. K., The Theory of  $A_{p}^{q}$  Spaces, PhD Thesis, University of Adelaide, South Australia, 1995.Google Scholar
Dunford, N. and Schwartz, J., Linear Operators, Vols I & 2 (Interscience, New York, 1958).Google Scholar
Fontenot, R. A. and Schochetman, I., ‘Induced representations of groups on Banach spaces’, Rocky Mountain J. Math. 7(1) (1977), 53–82.Google Scholar
Gaal, S. A., Linear Analysis and Representation Theory (Springer, Berlin, 1973).Google Scholar
Jaming, P. and Moran, W., ‘Tensor products and p-induction of representations on Banach spaces’, Collect. Math. 51(1) (2000), 83–109.Google Scholar
Kleppner, A., ‘Intertwining forms for summable induced representations’, Trans. Amer. Math. Soc. 112 (1964), 164–183.Google Scholar
Mackey, G. W., ‘On induced representations of groups’, Amer. J. Math. 73 (1951), 576–592.Google Scholar
Mackey, G. W., ‘Induced representations of locally compact groups I’, Ann. Math. (2) 55(1) (1952), 101–140.Google Scholar
Mautner, F. I., ‘A generalization of the Frobenius reciprocity theorem’, Proc. Natl. Acad. Sci. USA 37 (1951), 431–435.Google Scholar
Moore, C. C., ‘On the Frobenius reciprocity theorem for locally compact groups’, Pacific J. Math. 12 (1962), 359–365.Google Scholar