Research Article
Group closures of one-to-one transformations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-188
-
- Article
-
- You have access
- Export citation
When do finite Blaschke products commute?
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-200
-
- Article
-
- You have access
- Export citation
Certain inequalities for submanifolds in (K,μ)-contact space forms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-212
-
- Article
-
- You have access
- Export citation
Convergence theorems for topological group valued measures on effect algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-231
-
- Article
-
- You have access
- Export citation
On the operators which are invertible modulo an operator ideal
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 233-243
-
- Article
-
- You have access
- Export citation
A question of Paul Erdös and nilpotent-by-finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-254
-
- Article
-
- You have access
- Export citation
Abelian groups that are torsion over their endomorphism rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-263
-
- Article
-
- You have access
- Export citation
A duality proof of sampling localisation in relaxation spectrum recovery
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 265-269
-
- Article
-
- You have access
- Export citation
A note on the ideals of groupoid C*-algebras from Smale spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-279
-
- Article
-
- You have access
- Export citation
Integrated solutions of stochastic evolution equations with additive noise
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 281-290
-
- Article
-
- You have access
- Export citation
On the set of Hilbert polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-305
-
- Article
-
- You have access
- Export citation
Decomposability of finite rank operators in certain subspaces and algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-314
-
- Article
-
- You have access
- Export citation
Coprime actions and degrees of primitive inducers of invariant characters
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-320
-
- Article
-
- You have access
- Export citation
Macmahon's partition analysis IX: K-gon partitions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-329
-
- Article
-
- You have access
- Export citation
Non-periodic continued fractions in hyperelliptic function fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-343
-
- Article
-
- You have access
- Export citation
Some metric properties of Lüroth expansions over the field of Laurent series
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-351
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 64 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 64 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

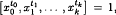 , where
, where 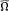
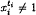 . Let
. Let 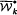 the class of all groups
the class of all groups 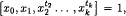 , where
, where 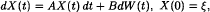 in the case when
in the case when