Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T02:14:48.886Z Has data issue: false hasContentIssue false
  • English
  • Français

A question of Paul Erdös and nilpotent-by-finite groups

Published online by Cambridge University Press:  17 April 2009

Bijan Taeri
Bijan Taeri
Affiliation:
Department of Mathematics, Isfahan University of Technology, Isfahan and Institute for Studies in Theoretical Physics and Mathematics, Iran, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let n be a positive integer or infinity (denoted ∞), k a positive integer. We denote by Ωk(n) the class of groups G such that, for every subset X of G of cardinality n + 1, there exist distinct elements x, y ∈ X and integers t0, t1…, tk such that 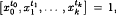, where xi, ∈ {x, y}, i = 0, 1,…,k, x0 ≠ x1. If the integers t0, t1,…,tk are the same for any subset X of G, we say that G is in the class 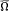k(n). The class k (n) is defined exactly as Ωk(n) with the additional conditions 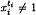. Let t2, t3,…,tk be fixed integers. We denote by 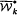the class of all groups G such that for any infinite subsets X and Y there exist x ∈ X, y ∈ Y such that 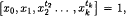, where xi ∈ {x, y}, x0 ≠ x1, i = 2, 3, …, k. Here we prove that (1) If G ∈ k(2) is a finitely generated soluble group, then G is nilpotent.

(2) If G ∈ Ωk(∞) is a finitely generated soluble group, then G is nilpotentby-finite.

(3) If G ∈ 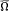k(n), n a positive integer, is a finitely generated residually finite group, then G is nilpotent-by-finite.

(4) If G is an infinite 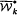-group in which every nontrivial finitely generated subgroup has a nontrivial finite quotient, then G is nilpotent-by-finite.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 64 , Issue 2 , October 2001 , pp. 245 - 254
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Abdollahi, A.„ ‘Some Engel conditions on infinite subsets of certain groups’, Bull Austral. Math. Soc. 62 (2000), 141–148.CrossRefGoogle Scholar
[2]Abdollahi, A., ‘Some Engel conditions on finite subsets of certain groups’, Houston J. Math. (to appear).Google Scholar
[3]Abdollahi, A. and Taeri, B., ‘A condition on finitely generated soluble groups’, Comm. Algebra 27 (1999), 5633–5638.CrossRefGoogle Scholar
[4]Abdollahi, A. and Taeri, B., ‘A condition on certain variety of groups’, Rend. Sem. Mat. Univ. Padova 104 (2000), 129–134.Google Scholar
[5]Abdollahi, A. and Taeri, B., ‘Some conditions on infinite subsets of infinite groups’, Bull. Malaysian Math. Soc. 22 (1999), 87–93.Google Scholar
[6]Abdollahi, A. and Taeri, B., ‘On a class of infinite rings’, Algebra Colloq. (to appear).Google Scholar
[7]Delizia, C., Smith, H. and Rhamtulla, A.H., ‘Locally graded groups with a nilpotency condition on infinite subsets’, J. Austral. Math. Soc. Ser. A 69 (2000), 415–420.CrossRefGoogle Scholar
[8]Endimioni, G., ‘Groups covered by finitely many nilpotent subgroup’, Bull. Austral Math. Soc. 50 (1994), 459–464.CrossRefGoogle Scholar
[9]Endimioni, G., ‘Groupes finis satisfaisant la condition (,n)’, C. R. Acad. Sci. Paris. Série I 319 (1994), 1245–1247.Google Scholar
[10]Endimioni, G., ‘On a combinatorial problem in varieties of groups’, Comm. Algebra 14 (1995), 5297–5307.CrossRefGoogle Scholar
[11]Kim, P.S. and Rhemtulla, A.H., ‘Permutable word products in groups’, Bull. Austral. Math. Soc. 40 (1989), 243–254.CrossRefGoogle Scholar
[12]Kim, Y.K. and Rhemtulla, A.H., ‘Weak maximality condition and polycyclic groups’, Proc. Amer. Math. Soc. 123 (1995), 711–714.CrossRefGoogle Scholar
[13]Kim, P.S., Rhemtulla, A. and Smith, H., ‘A characterization of infinite metabelian groups’, Houston. J. Math. 17 (1991), 129–137.Google Scholar
[14]Kropholler, P.H., ‘Groups with no large wreath product section’, Proc. London Math. Soc. 3 (1984), 155–169.CrossRefGoogle Scholar
[15]Lennox, J. and Wiegold, J., ‘Extension of a problem of Paul Erdős on groups’, J. Austral. Math. Soc. Ser. A 31 (1981), 451–463.CrossRefGoogle Scholar
[16]Longobardi, P. and Maj, M., ‘Finitely generated soluble groups with an Engel condition on infinite subsets’, Rend. Sem. Mat. Univ. Padova 89 (1993), 97–102.Google Scholar
[17]Longobardi, P., Maj, M. and Rhemtulla, A.H., ‘Infinite group in a given variety and Ramsey's Theorem’, Comm. Algebra 20 (1992), 127–139.CrossRefGoogle Scholar
[18]Neumann, B.H., ‘Twisted wreath products of groups’, Arch. Math. (Basel) 123 (1963), 1–6.CrossRefGoogle Scholar
[19]Neumann, B.H., ‘A problem of Paul Erdős on groups’, J. Austral. Math. Soc. Ser. A 21 (1976), 467–472.CrossRefGoogle Scholar
[20]Puglisi, O. and Spiezia, L.S., ‘A combinatorial property of certain infinite groups’, Comm. Algebra 22 (1994), 1457–1465.CrossRefGoogle Scholar
[21]Robinson, D.J.S., Finiteness conditions and generalized soluble groups, Part I (Springer-Verlag, Berlin, Heidelberg, New York, 1972).CrossRefGoogle Scholar
[22]Robinson, D.J.S., A course in the theory of groups (Second edition), Graduate Texts in Mathematics 80 (Springer-Verlag, Berlin, Heidelberg, New York, 1996).CrossRefGoogle Scholar
[23]Spiezia, L.S., ‘A property of the variety of 2-Engel groups’, Rend. Sem. Mat. Univ. Padova 91 (1994), 225–228.Google Scholar
[24]Spiezia, L.S., ‘A characterization of third Engel groups’, 1Arch. Math. 64 (1995), 369–373.CrossRefGoogle Scholar
[25]Taeri, B., ‘A combinatorial condition on a certain variety of groups’, Arch. Math. (Basel) (to appear).Google Scholar
[26]Tomkinson, M.J., ‘Hypercenter-by-finite groups’, Publ. Math. Debrecen 40 (1992), 383–417.Google Scholar
[27]Trabelsi, N., ‘Characterisation of nilpotent-by-finite groups’, Bull. Austral. Math. Soc. 61 (2000), 33–38.CrossRefGoogle Scholar
[28]Wilson, J.S., ‘Two generator condition in residually finite groups’, Bull. London Math. Soc. 23 (1991), 239–248.CrossRefGoogle Scholar