In this paper we consider the problem of an upper bound estimate for the least quadratic non-residue modulo prime number on special arithmetic sequences such as f(n) = [αn] and f(n) = [nc].

We study Kalton's theorem on the unconditional convergence of series of compact operators and we use some matrix techniques to obtain sufficient conditions, weaker than previous ones, on the convergence and unconditional convergence of series of compact operators. Finally, we characterise weak unconditionally Cauchy series in Cℒ(X, Y) in the terms of certain spaces of vector sequences.

In this paper, we investigate a public key cryptosystem which is derived from a third order linear recurrence relation and is analogous to the RSA and LUC cryptosystems. The explicit formulation involves a generalisation of the rule for composition of powers and of the calculus of the Euler totient function which underlie the algebra of the RSA cryptosystem. The security of all these systems appears to be comparable and to depend on the intractability of factorization but the systems do not seem to be mathematically equivalent.

On montre que la partie nilpotente d'une solveriété d'Einstein standard, dont le type de valeur propre est égal à (1 < 2; d1, d2), est nécessairement indécomposable si d1 et d2 sont premiers entre eux.

This paper is devoted to the study of a class of generalised P-nilpotent groups in the universe c of all radical locally finite groups satisfying min-q for every prime q. Some results of finite groups are extended and a characterisation of the injectors associated with this class is given.

In 1988 Howie, Robertson and Schein characterised the transformations of a finite set X that can be written as a product of two or of three idempotent transformations of X; and in 1989 Saito did the same for products of four idempotents. In 1998 Thomas extended the characterisation of two idempotents to arbitrary sets, and here we characterise products of three idempotents in general. We also define a notion of complexity for transformations of any set and use it to provide a different solution to the three-idempotent problem.

This note relates polynomial remainders with polynomial automorphisms of the plane. It also formulates a conjecture, equivalent to the famous Jacobian Conjecture. The latter provides an algorithm for checking when a polynomial map is an automorphism. In addition, a criterion is presented for a real polynomial map to be bijective.

We study interior C1,1 regularity of generalised solutions of the Monge-Ampére equation det D2u = ψ, ψ ≥ 0, on a bounded convex domain Ω in ℝn with u = ϕ on ∂Ω. We prove in particular that u ∈ C1,1(Ω) if either i) ϕ = 0 and ψ1/(n − 1) ∈ C1,1 (Ω) or ii) Ω is C1,1 strongly convex, ϕ ∈ C1,1 (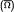), ψ1/(n − 1) ∈ C1,1(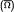) and ψ > 0 on U ∩ Ω, where U is a neighbourhood of ∂Ω. The main tool is an improvement of Pogorelov's well known C1,1 estimate so that it can be applied to the degenerate case.

A multiplier rule is given as a necessary optimality condition for proper minimality in set-valued optimisation. We use derivatives in the sense of the lower Dini derivative for the objective set-valued map and the set-valued maps defining the constraints.

Let m be an odd positive integer greater than 2 and f the smallest positive integer such that 2f ≡ 1 (mod m). It is proved that every algebraic integer in the cyclotomic field ℚ(ζm) can be expressed as a sum of three integral squares if and only if f is even.

Dedicated to the memory of Bernhard H. Neumann

Not often is a formation also a Fitting class. In this article groups are exhibited that are contained in a given saturated formation and that do not lead out of this formation by forming normal products with other groups of it. This generalises a result of Cossey on T-groups and supersolvable groups.

In this paper, we show that the Robinson, Nguyen–Strodiot–Mifflin and Jourani constraint qualifications are sufficient conditions for invexity of constrained functions with respect to the same scale function in Lipschitzian mathematical programmings. A Kuhn-Tucker necessary optimality condition is also given under the constraint qualification on the invexity property of constrained functions.

Tensor products of divisible effect algebras and tensor products of the corresponding universal groups are studied. It is shown that the universal group of the tensor product of divisible effect algebras is (isomorphic to) the tensor product of the corresponding universal groups. Moreover, it is shown that the tensor product of two unit intervals [0, 1] of real numbers is not a lattice.

The main purpose of this paper is to exhibit a doubly-infinite family of examples which are extensions of a p-group by a p′-group, with the action satisfying some conditions of Zappa (1951), arising from his study of dual-standard (meet-distributive) subgroups. The examples show that Zappa's conditions do not bound the nilpotency class (or even the derived length) of the p-group. The key to this work is found in closely related conditions of Hartley (published here for the first time). The examples use some exceptional relationships between primes.

Using results from topological groups and topological dynamics for locally compact spaces, Aoki has shown that when a group automorphism of a locally compact totally disconnected group is ergodic under the Haar measure, the group is compact. We provide some remarks on Aoki's proof. Also we present a new proof of his result using the structure of locally compact totally disconnected groups established by Willis.

This paper Presents a multivalued version of an approximation result of Ky Fan (Math. Z.112 (1969)) for maps.

A linear mapping T from a subspace E of a Banach algebra into another Banach algebra is called spectrally bounded if there is a constant M ≥ 0 such that r(T x) ≤ Mr(x) for all x ∈ E, where r (·) denotes the spectral radius. We establish the equivalence of the following properties of a unital linear mapping T from a unital C* -algebra A into its centre:

(a) T is spectrally bounded;

(b) T is a spectrally bounded trace;

(c) T is a bounded trace.