Research Article
Weighted normal numbers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-181
-
- Article
-
- You have access
- Export citation
A note on resonance problems with nonlinearity bounded in one direction
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 183-188
-
- Article
-
- You have access
- Export citation
Morita duality and finitely group-graded rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-194
-
- Article
-
- You have access
- Export citation
On the magnitude of integer points on elliptic curves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 195-199
-
- Article
-
- You have access
- Export citation
Approximate polyhedra, density and discrete maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-206
-
- Article
-
- You have access
- Export citation
Strong barrelledness properties in B(Σ, X)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-214
-
- Article
-
- You have access
- Export citation
Unicity theorems for meromorphic or entire functions II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-224
-
- Article
-
- You have access
- Export citation
Remarks on symmetric smooth norms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 225-229
-
- Article
-
- You have access
- Export citation
Simple modules over the coordinate ring of quantum affine space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-234
-
- Article
-
- You have access
- Export citation
Some utility theorems on inductive limits of preordered topological spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 235-246
-
- Article
-
- You have access
- Export citation
On Ky Fan's covering theorems for simplexes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-252
-
- Article
-
- You have access
- Export citation
Soluble and linear repetitive groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-261
-
- Article
-
- You have access
- Export citation
Partial clones containing all permutations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-278
-
- Article
-
- You have access
- Export citation
Remarks on a measure of weak noncompactness in the Lebesgue space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-286
-
- Article
-
- You have access
- Export citation
Curvature evolution of plane curves with prescribed opening angle
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 287-296
-
- Article
-
- You have access
- Export citation
Free Abelian topological groups and the Pontryagin-Van Kampen duality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 297-311
-
- Article
-
- You have access
- Export citation
On the splitting field of the Alexander polynomial of a periodic knot
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-315
-
- Article
-
- You have access
- Export citation
Discrete product systems with twisted units
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-326
-
- Article
-
- You have access
- Export citation
Note on amenable algebras of operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 327-329
-
- Article
-
- You have access
- Export citation
Finding eisenstein elements in cyclic number fields of odd prime degree
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-340
-
- Article
-
- You have access
- Export citation

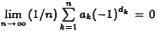 for almost every 0 <
for almost every 0 < 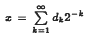 is the dyadic expansion of
is the dyadic expansion of 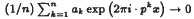 almost everywhere where
almost everywhere where 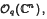 , the coordinate ring of quantum affine space, are classified in the case when
, the coordinate ring of quantum affine space, are classified in the case when