Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rodríguez-Rorno, Suemi
1999.
Actions of the dipper-donkin quantizationGL2on the clifford algebraC(l,3).
Communications in Algebra,
Vol. 27,
Issue. 9,
p.
4307.
Kharchenko, V.K.
Keller, Jaime
and
Rodríguez-Romo, S.
1999.
Actions ofGLq(2,C) onC(1,3) and its four dimensional representations.
Communications in Algebra,
Vol. 27,
Issue. 4,
p.
1843.
Bera, Sanu
Mandal, Sugata
and
Nandy, Soumendu
2024.
Quantum Heisenberg enveloping algebras at roots of unity.
Journal of Algebra,
Vol. 649,
Issue. ,
p.
223.


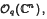 , the coordinate ring of quantum affine space, are classified in the case when
, the coordinate ring of quantum affine space, are classified in the case when 