Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 2
Optimal commissions and subscriptions in mutual aid platforms
-
- Published online by Cambridge University Press:
- 04 July 2023, pp. 658-683
-
- Article
- Export citation
- Cited by 2
TAXATION OF A GMWB VARIABLE ANNUITY IN A STOCHASTIC INTEREST RATE MODEL
-
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1001-1035
-
- Article
- Export citation
- Cited by 2
On Pareto Conjugate Priors and Their Application to Large Claims Reinsurance Premium Calculation
-
- Published online by Cambridge University Press:
- 17 April 2015, pp. 405-428
-
- Article
-
- You have access
- Export citation
- Cited by 2
A Pricing Model in a Sensitive Insurance Market
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 135-149
-
- Article
-
- You have access
- Export citation
- Cited by 2
On The Estimation of Means and Variances In The Case Of Unequal Components
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 323-335
-
- Article
-
- You have access
- Export citation
- Cited by 2
PORTFOLIO INSURANCE STRATEGIES FOR A TARGET ANNUITIZATION FUND
-
- Published online by Cambridge University Press:
- 01 July 2020, pp. 873-912
-
- Article
- Export citation
- Cited by 2
A Simulation Procedure for Comparing Different Claims Reserving Methods
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 191-216
-
- Article
-
- You have access
- Export citation
- Cited by 2
Insurance Capital as a Shared Asset
-
- Published online by Cambridge University Press:
- 17 April 2015, pp. 471-486
-
- Article
-
- You have access
- Export citation
- Cited by 2
Survival Probabilities Based on Pareto Claim Distributions: Comment
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 154-157
-
- Article
-
- You have access
- Export citation
- Cited by 2
Signature-based validation of real-world economic scenarios
-
- Published online by Cambridge University Press:
- 04 April 2024, pp. 410-440
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 2
Estimating the VaR-induced Euler allocation rule
-
- Published online by Cambridge University Press:
- 02 May 2023, pp. 619-635
-
- Article
- Export citation
- Cited by 2
On Changing the Parameter of Exponential Smoothing in Experience Rating
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 191-200
-
- Article
-
- You have access
- Export citation
- Cited by 2
DYNAMIC ASSET ALLOCATION FOR TARGET DATE FUNDS UNDER THE BENCHMARK APPROACH
-
- Published online by Cambridge University Press:
- 29 March 2021, pp. 449-474
-
- Article
- Export citation
- Cited by 2
Collective Theory of Risk and Utility Functions
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 6-10
-
- Article
-
- You have access
- Export citation
- Cited by 2
Obituary on Bruno de Finetti
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 11-12
-
- Article
-
- You have access
- Export citation
- Cited by 2
VALUATION OF MORTGAGE INSURANCE CONTRACTS WITH COUNTERPARTY DEFAULT RISK: REDUCED-FORM APPROACH
-
- Published online by Cambridge University Press:
- 11 March 2014, pp. 303-334
-
- Article
- Export citation
- Cited by 2
The Future of ASTIN*
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 75-80
-
- Article
-
- You have access
- Export citation
- Cited by 2
OPTIMAL CONTROL OF THE DECUMULATION OF A RETIREMENT PORTFOLIO WITH VARIABLE SPENDING AND DYNAMIC ASSET ALLOCATION
- Part of:
-
- Published online by Cambridge University Press:
- 28 July 2021, pp. 905-938
-
- Article
- Export citation
- Cited by 2
A DOUBLE COMMON FACTOR MODEL FOR MORTALITY PROJECTION USING BEST-PERFORMANCE MORTALITY RATES AS REFERENCE
-
- Published online by Cambridge University Press:
- 01 February 2021, pp. 349-374
-
- Article
- Export citation
- Cited by 2
The Application of Expected-Utility Theory to the Choice of Investment Channels in a Defined-Contribution Retirement Fund
-
- Published online by Cambridge University Press:
- 09 August 2013, pp. 615-647
-
- Article
- Export citation

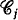 .
.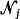 independent risks
independent risks 
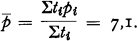
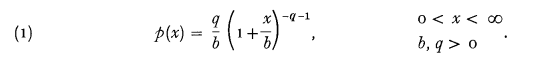
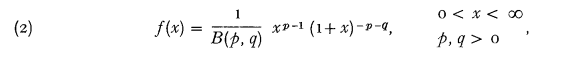
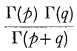 is the beta function.
is the beta function.