Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T00:57:57.429Z Has data issue: false hasContentIssue false
  • English
  • Français

A Pricing Model in a Sensitive Insurance Market

Published online by Cambridge University Press:  29 August 2014

Franco Moriconi
Franco Moriconi*
Affiliation:
Institute of Mathematics, University of Rome
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A great attention has been devoted, in the actuarial literature, to premium calculation principles and it has been often emphasized that these principles should not only be defined in strictly actuarial terms, but should also take into account the market conditions (Bühlmann (1980), de Jong (1981)).

In this paper we propose a decision model to define the pricing policy of an insurance company that operates in a market which is stratified in k risk classes .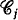

It is assumed that any class constitutes a homogeneous collective containing 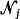independent risks Sj(t) of compound Poisson type, with the same intensity λj. The number nj of risks of 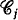that are held in the insurance portfolio depends on the premium charged to the class by means of a demand function which captures the concept of risk aversion and represents the fraction of individuals of 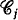, that insure themselves at the annual premium xj.

With these assumptions, the return Y on the portfolio is a function of the vector x = (x1, x2, …, xk) of the prices charged to the single classes (and of the time) and x is therefore the decision policy instrument adopted by the company for the selection of the portfolio, whose optimal composition is evaluated according to a risk-return type performance criterion.

As a measure of risk we adopt the ultimate ruin probability q(w) that, in the assumptions of our model, can be related to a safety index τ, by means of Lundberg-de Finetti inequality. Even though it has been widely debated in the actuarial field, the use of q(w) offers undeniable operational advantages. In our case the safety index τ can be expressed as a function of x and therefore, in the phase of selecting an efficient portfolio, it becomes the function to be maximized, for a given level M of the expected return.

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 13 , Issue 2 , December 1982 , pp. 135 - 149
Copyright
Copyright © International Actuarial Association 1982

References

REFERENCES

Ammeter, H. (1970) Das Solvibilitätsproblera in der Risiko-Lebenversicherung, Mitteilungen der Vereinigung schweizerischer Versicherungsmathematiker 70, 41–56.Google Scholar
Ammeter, H., Depoid, P. and de Finetti, B. (1959) L'Étude Mathématique des Assurances Non Viagères dans l'Europe Continentale Occidentale. Astin Bulletin 1, 46–70.CrossRefGoogle Scholar
Amsler, M.-H. (1978) L'equation générale d'équilibre d'un risque collectif. Mitteilungen der Vereinigung schweizerischer Versicherugsmathematiker 78, 221–246.Google Scholar
Bühlmann, H. (1980) An Economic Premium Principle. Astin Bulletin 11, 52–60.CrossRefGoogle Scholar
Cacciafesta, R. (1970) Sulla Determinazione delle Classi di Rischio. Giornale dell'Istituto Italiano degli Attuari 70, 38–48.Google Scholar
Dubourdieu, J. (1952) Théorie Mathématiques des Assurances. I, Théorie Mathématique du Risque dans les Assurances de Répartition. Gauthier-Villars: Paris.Google Scholar
Ferra, C. de (1968) Sulla Vantaggiosità delle Operazioni Assicurative, Giornale dell'Istituto Italiano degli Attuari 68, 1–16.Google Scholar
Finetti, B. de (1939) La Teoria del Rischio e il Problema della “Rovina dei Giocatori”. Giornale dell'Istituto Italiano degli Attuari 39, 41–51.Google Scholar
Gerber, H. U. (1981) On the Probability of Ruin in an Autoregressive Model. Mitteilungen der Vereinigung schweizerischer Versicherungsmathematiker 81, 213–219.Google Scholar
Jong, P. de (1981) Insurance Premiums under Demand Constraints. Scandinavian Actuarial Journal 81, 123–125.CrossRefGoogle Scholar
Kahane, Y. (1979) The Theory of Insurance Risk Premiums—A Re-examination in the Light of Recent Developments in Capital Market Theory. Astin Bulletin 10, 223–239.CrossRefGoogle Scholar
Lundberg, F. (1909) Über die Theorie der Rückversicherung. Trans. VI Intern. Congr. Act. 1, 877–948.Google Scholar
Massé, P. (1964) Le Choix des Investissements (Critéres et Méthodes). Dunod: Paris.Google Scholar
Pressacco, F. (1979) Value and Prices in a Reinsurance Market. Astin Bulletin 10, 263–273.CrossRefGoogle Scholar
Rothschild, M. and Stiglitz, J. (1976) Equilibrium in Competitive Insurance Markets: an Essay on the Economies of Perfect Information. Quarterly Journal of Economics 90, 629–649.CrossRefGoogle Scholar
Seal, H. L. (1979) Survival Probabilities (The Goal of Risk Theory). Wiley: New York.Google Scholar
Sengupta, J. K. (1981) Optimal Decisions under Uncertainty. Lecture Notes in Economics and Mathematical Systems N.193, Springer-Verlag: Berlin.CrossRefGoogle Scholar
Volpe di Prignano, E. (1974) Sulla Misurabilità del Premio di Indifferenza nei Rami Elementari. Giornale dell'Istituto Italiano degli Attuari 74, 25–45.Google Scholar