Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T23:33:00.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On The Estimation of Means and Variances In The Case Of Unequal Components

Published online by Cambridge University Press:  29 August 2014

Esa Hovinen
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In practical statistical work one frequently meets certain problems. For instance, we may have the following data about loss ratios in certain insurance companies and corresponding, numbers of insurance in force:

I assume further that we have no reason to believe that the companies, their loss ratios and their structure of insurances in force differ in any other way than by the size of companies. The problem is how to get quick estimates of mean losses and their variances in different companies?

A straitforward way to estimate the mean loss ratio would be to compute the usual mean of numbers pi, (Σpi/6) = 14; its standard deviation is 6,5. As this procedure of the “first statistician” seems to be too simple and naive, a “more cautious” statistician would compute the weighted mean loss ratio

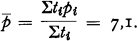
The “more cautious” statistician would arque that his result is much better than the other result 14. But what would be the variance of the estimate 7,1, and what is the variance in the different companies?

Type
Research Article
Information
ASTIN Bulletin: The Journal of the IAA , Volume 8 , Issue 3 , September 1975 , pp. 323 - 335
Copyright
Copyright © International Actuarial Association 1975

References

1) In his book Feller uses vocabulary differing from the one used here. The most important difference is between GPP and CPP; with CPP Feller means GPP used here.